How to tell if someone is a crackpot

Page last updated 13 June 2022

How can you tell if someone is a crank/crackpot?

It’s easy - if they really are a crank/crackpot, then they will make non-trivial errors of fact or errors of logic, or both. So all you have to do is to show that they are making such errors.

However, many people like to think that there are other ways of deciding if someone is a crank/crackpot, by looking at every other aspect of the alleged crank/crackpot rather than the errors they make (see also Cranks and Crackpots). This is rather like a jury deciding by only looking at circumstantial evidence and refusing to consider the first-hand evidence - which any reasonable person would deem to be absurd.

But if someone really is a crank/crackpot, it’s a simple matter to find non-trivial errors in their pronouncements.

The crackpot John Gabriel

As an example, let’s consider the case of the alleged crackpot John Gabriel. Gabriel has a YouTube presence with over 150 videos, see John Gabriel’s YouTube Videos, as well as other webpages.

The Error in Gabriel’s “New Calculus”

Gabriel has several webpages devoted to a notion of his called the New Calculus. On his webpage The New Calculus you can find the following claim:

Gabriel states that a line that is parallel to the tangent line is given by::

[{ f (x + n) − f (x − m) }/(m + n)] x + p

This, as it stands, is a formula where the variables x, m and n are independent variables - i.e: there is no indication that the value of one of them is dependent on the other.

But, for any given x, all parallel lines must have the same gradient, which means that for all such parallel lines, the value of f (x + n) − f (x − m) }/(m + n) must be a fixed value. And for that to be the case, for a given value of x, the values m and n cannot be arbitrary - i.e: the values of x, m and n are interdependent. For example, given a specific x, and any specific value for n, then the point m must be such that it is the intersection of:

a) a straight line through n which has the gradient of f ′(x)

and

b) the function f (x).

Gabriel defines f ′(x) in terms of m and n. But for any given n, the value of m depends on the value of f ′(x) - which itself depends on the value of m. (Footnote: Similarly, for any given m, the value of n depends on the value of f ′(x), which in turn depends on the value of n.)

This is Gabriel’s error - he hasn’t actually provided any general means of determining the derivative of a function, since his definition of the derivative is itself defined in terms of the derivative.

In his demos, Gabriel conveniently chooses simple formulas for which his method appears to give a method for calculating the correct value of a derivative. But for most other formulas it doesn’t. For an example, let’s use a formula that Gabriel himself uses to rubbish conventional calculus, such as in his video There are no tangent lines at points of inflection. Here he uses the formula:

x³ + 2x² − x + 1 , see the graph below, where the equation is black solid, the first derivative is dashed blue, an inflection point is a black circle, and the tangent at this point is dashed red.

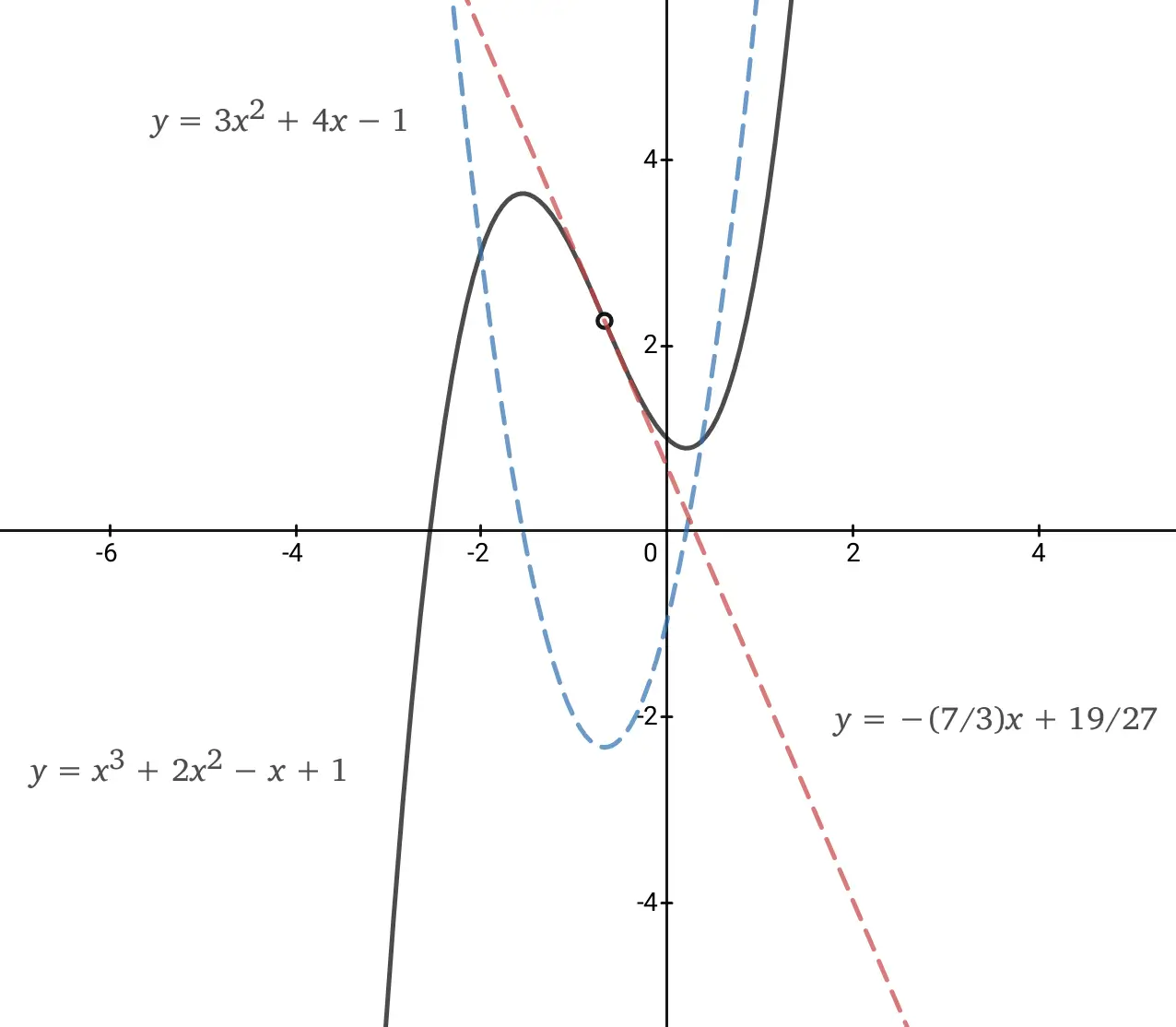
Applying Gabriel’s method to this formula, we get that the derivative is:

(m³ + 3m²x − 3m x² + n³ + 3n²x + 3n x² − 2m² + 4m x + 2n² + 4n x − m − n)/(m + n)

simplifying by dividing the numerator by m + n, this gives the derivative as:

m² − mn − 3mx − 2m + n² + 3nx + 2n + 3x² + 4x − 1

So - how does that give a value for the derivative? (Footnote: John Gabriel pointed out some plus/minus typos in the original. But of course, that makes no difference whatsoever to the key point, which is that Gabriel’s equation does not give a value for the derivative.)

Answer: it doesn’t. You would need to know values for both m and n, and as explained above, that would require that you already know the value of the derivative. And at the inflection point at (⁻²⁄₃ , ⁶¹⁄₂₇ ), there are no possible values of m and n, and if we were to set m = n = 0, we would then be dividing by zero, the very thing that Gabriel complains (wrongly) about in standard calculus! Gabriel tries to get around this fatally crippling problem in his “New Calculus” by denying that there is a tangent line at the inflection point, since he thinks that a tangent line should extend to both sides of a point and locally only be to one side of the curve. But how does Gabriel know where there are inflection points? Normal mathematics says that there are inflection points where the derivative reaches a local maximum or a local minimum (as at x = ⁻²⁄₃ in the graph above) - which is when the second derivative has a value of zero. But in Gabriel’s incredibly convoluted “New Calculus”, a derivative can never have any local maximum nor a local minimum value, and a second derivative can never have a value of zero.

So, according to Gabriel, a nice smooth sine wave doesn’t have a slope that changes smoothly - according to Gabriel, at two points in each cycle, the curve doesn’t have a slope (circled points above) but everywhere else a slope exists for the curve and changes nice and smoothly. (Footnote: On the other hand, if we set m = n in the above, this is the same as obtaining the derivative as:
Lim_h→0  ( f (x + h) − f (x − h) )/2h
and we get the standard conventional result:
Lim_h→0   h²+3x² + 4x − 1
from which we get the correct derivative as:
3x² + 4x − 1. )

And another consequence of Gabriel’s suppositions is that his marvelous “New Calculus” method of calculating the derivative of a function by his wonderful “auxiliary equation” can’t even be used to find the derivative of the simplest type of function possible - a straight line - since Gabriel’s method requires that there exist lines that have the same slope as the derivative but have to cross the function curve at two points.

Yes, Gabriel’s “New Calculus” is a joke - or a parody.

Gabriel’s error regarding the definition of a derivative

Gabriel also manages to completely misunderstand conventional calculus, as he demonstrates in his video A simple comparison between New Calculus and bogus mainstream Calculus. First he correctly states the conventional derivation of a derivative for a function x², like this:

f ′(x)   =   Lim_h→0  ( f (x + h) − f (x) )/h

=   Lim_h→0   (x² + 2xh + h² − x²)/h

=   Lim_h→0  (2xh + h²)/h

=   Lim_h→0   2x + h

But then he claims that the above conventional derivation of a derivative implies, for the case where x = 2, that:

f ′(x)   =   Lim_10→0   ( f (2 + 10) − f (2) )/10

=   Lim_10→0   (144 − 4)/10 = 14

where he fixes the variable h as 10 and then thinks that conventional calculus gives the result 14 simply because he has written Lim_10→0.

But Gabriel’s error is that, on the one hand, he treats “10” as a fixed value, but on the other hand, at the same time he treats it as a variable that can vary since he states 10→0. That is patently absurd.

( f (x + h) − f (x) )/h is simply a function with two variables, x and h. And all we do when we want x to take the value 2 is that we substitute 2 for x. That’s all - we don’t change anything else (which is what Gabriel does). And so the correct formulas for x = 2 are:

f ′(2)   =   Lim_h→0  ( f (2 + h) − f (2) )/h

=   Lim_h→0  (2² + 2 · 2h + h² − 2²)/h

=   Lim_h→0  (4h + h²)/h

=   Lim_h→0   4 + h

Gabriel seems to think that there is a problem with the limit concept in the above; he thinks that it involves h taking the value of 0. But there isn’t any problem at all. For all h > 0, 4 + h cannot be less than 4, and for all h < 0, 4 + h cannot be greater than 4. Hence the limiting value of 4 + h for all h ≠ 0 is 4; it can’t be more than 4 and it can’t be less than 4. That’s all the limit concept involves.

Contrary to what Gabriel claims, there is no requirement that h takes the value 0. There is no trickery involved, there is no fudge.

Note that we can also talk about the derivative to the right-side or left-side of a point, see Appendix: Left and Right side derivatives below.

Gabriel’s error of logic

On his webpage Invalid Logical Disjunctions Gabriel demonstrates that he completely fails to understand simple basic fundamentals of logic.

He says:

“If you write m ≤ n that’s perfectly correct because neither n nor m are known … but if both of them are known it’s not correct.”

That is hilarious !     Gabriel is saying that m ≤ n is correct unless m and n are both substituted !

When you have finished mirthfully rolling about on the floor clutching your sides, we’ll continue.

Yes, it’s evident that Gabriel completely fails to understand the entire point of a generalization, which is that if it holds for all values of its free variables, then it holds for any values that are substituted for its free variables. (Footnote: Provided that the values belong to the domain of the variables.)

Conclusion

Well, it’s actually quite easy to show if someone really is a mathematical crackpot.

And yes, it is abundantly evident that John Gabriel is a complete crackpot - or else a very convincing joker.

For an analysis of another crackpot “proof ”, see Kalimuthu Sennimalai - Crackpot or Joker?

Appendix: Left and Right side derivatives

As an aside, I might point out here a bit of information regarding left-side derivatives and right-side derivatives. A right-side derivative is defined as:

f₊′(x) = Lim_h→0+   ( f (x + h) − f (x) )/h

and where h can only be positive, i.e: h > 0. The right-side derivative gives the gradient of a function to the right side of a given point.

 

The left-side derivative is defined as:

f₋′(x) = Lim_h→0−   ( f (x + h) − f (x) )/h

where h can only be negative, i.e: h < 0. The left-side derivative gives the gradient of a function to the left side of a given point.

 

For many functions the left-side and right-side derivatives are equal. But for some functions, they can be different, if there is a kink, an abrupt change of direction. (Footnote: Note: I am speaking informally here. You can find formal definitions elsewhere.) Before we go any further, perhaps I should point out that Gabriel denies that there can be such a thing as a piecewise function, see There are no piecewise functions, despite the fact that piecewise functions are frequently used in real world engineering calculations with successful results. It appears that Gabriel decides that he alone is the arbitrator of what is to be allowed in mathematical definitions.

 

Anyway, an example of such a function is given by the piecewise function:

 

 f (x) =

x²

   for  x ≤ 0

 

− x

   for  0 < x < 2

 

(x − 2)² − 2

   for  x ≥ 2

 

 

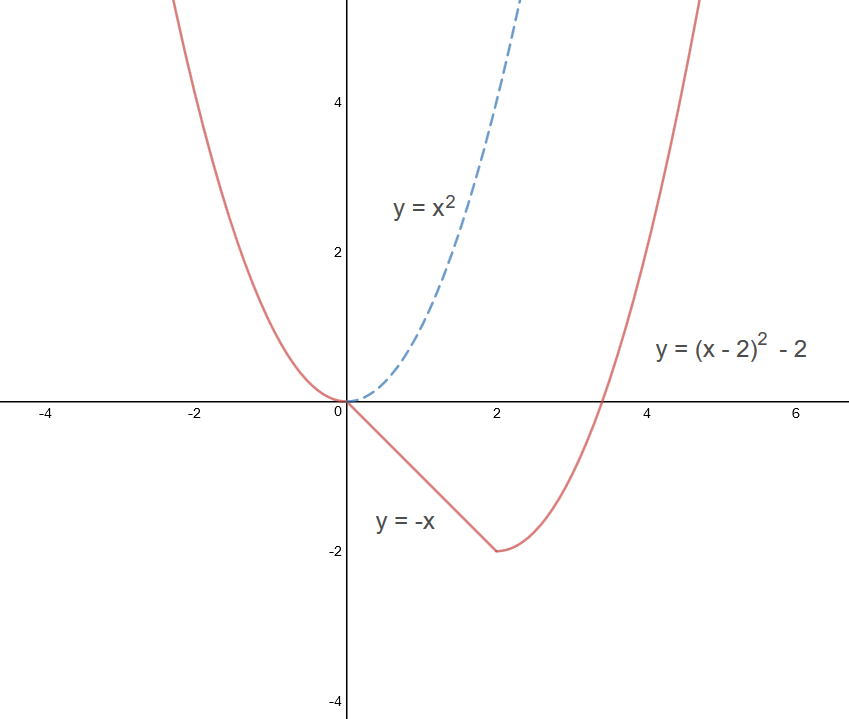
The derivative at the point (0, 0) for the function y = x² (for all x) is 0.

 

At the point (0, 0), the left-side derivative of the above function f (x) is 0, since the function f (x) is x² to the left of 0. The right-side derivative is − 1, since the function f (x) is − x to the right of 0.

 

Similarly, at the point (−2, −2) the left-side derivative of f (x) is − 1 and the right-side derivative is 0.

Footnotes: