The Courant & Robbins Contradiction
Page last updated 06 Oct 2023

In the book, What is Mathematics? by Courant and Robbins,
Herbert Robbins and Richard Courant, Courant & Robbins, What is mathematics? pub: Oxford University Press, New York, 2nd ed. 1996, Ch 4, Section 2, pp.82-83. ISBN10: 0195105192. (First edition, 1941).
there is a proof that there are more real numbers than natural numbers, a proof that, intriguingly, is not based on one of Georg Cantor’s well-known proofs. It appears that it was Courant and Robbins who originally came up with the proof, although it can be seen mentioned elsewhere.
Sondheimer & Rogerson, Numbers and Infinity, pub: Cambridge University Press, 1st ed, 1981, ISBN10: 0521284333, Ch 11, pp.152-153 Numbers and Infinity: details.
Gregory Chaitin has made several references to the proof, see:
a) Chaitin, Algorithmic Information Theory, pub: Cambridge University Press, 2004, ISBN13: 9780521616041 (Section 7.1), this part of the book is based on Chaitin’s 1987 paper ‘Incompleteness theorems for random reals’.
b) Chaitin, Thinking about Gödel and Turing, Essays on Complexity, 1970-2007, pub: World Scientific Publishing Co. Pte. Ltd. ISBN13 9789812708953 (Section 2.2: Alternate proof: Any countable/denumerable set of reals has measure zero.)
c) Chaitin, Meta Math, The Quest for Omega, pub: Pantheon, First Edition, 2005, ISBN13: 9780375423130 (Chapter Five, Section: ‘Reals are uncomputable with probability one’)
John Stillwell, in the book Roads to Infinity: The Mathematics of Truth and Proof (CRC Press, 2010 Roads to Infinity: details) claims that Carl Gustav Axel von Harnack was the first to come up with this proof in 1885; however he provides no reference to where one might find Harnack’s proof.
Note: A reader has suggested that this Courant and Robbins proof is actually a version of a proof by Borel, but this is not the case. Courant and Robbins specifically state that they have what they call an intuitive proof. They state that the differences in the measure given by the limit of a geometric series and the total measure is a contradiction. Since Courant and Robbins say it is intuitive, it is reasonable to take that to mean that the casual reader wouldn’t need to know anything about the details of Borel’s work, which would involve detailed knowledge of the background mathematics, but could intuitively “see” the result that Courant and Robbins considered to be intuitively obvious, where they mean that the intuitively obvious is that the difference in measures means that there must be “more” real numbers than natural numbers. Although Courant and Robbins admit that it’s not a fully worked proof and they say it would need more detailed treatment, if someone calls a proof intuitive, one is entitled to take that to mean that the fully worked version of the proof would essentially follow the intuitive notion in formal form, and not by some quite different method.
It is easy to demonstrate that the argument is inherently flawed. However, the interesting thing about it is that a logical analysis of the underlying argument shows that the Platonist belief in the independent ‘actual’ existence of limitlessly many mathematical entitles is inherently illogical, because it shows that that belief leads to a contradiction. It is interesting that Courant and Robbins says it is intuitive, and that reflects the way that many Platonists think of real numbers as being a “bigger” set than the rationals. The demonstration of the contradiction in the proof by Courant and Robbins serves to demonstrate the untenability of the Platonist viewpoint.
The Courant and Robbins proof goes like this:
- Suppose that there can be a list (for definition of what is meant by a list, see one-to-one correspondence) that includes all of the real numbers. For our purposes, we will only consider the real numbers between 0 and 1. For convenience we will use the concept of the real number line between 0 and 1, and which represents all the real numbers between 0 and 1. The ‘proof’ operates by enclosing every real number in the list between 0 and 1 by a small length of a line as follows:
- For the first real number in the supposed list of all real numbers, we make a line segment that is 1⁄10 wide, and which includes that real number (note that the number can be anywhere within this line segment).
- For the second real number in the list, make a line segment 1⁄100 wide, enclosing that real number.
- For the third real number in the list, make a line segment 1⁄1000 wide, enclosing that real number.
- And so on, through the list, for all the real numbers. As long as the appropriate real number is within the correct line segment, it is immaterial precisely where in that line segment it lies.
- The proof says that if every real number between 0 and 1 is actually in the list, then the entire line between 0 and 1 must be covered by this infinite series of line segments whose lengths get progressively smaller: 1⁄10, 1⁄100, 1⁄1000, 1⁄10000, 1⁄100000 …
- Of course, some of the line smaller segments may overlap. But, says the proof, even if there were no overlapping at all, the actual total length of all our line segments is the sum of all the lengths
1⁄10 + 1⁄100 + 1⁄1000 + 1⁄10000 + 1⁄100000 … - The proof says that the sum of all these lengths is 1⁄9 , because 1⁄10 + 1⁄100 + 1⁄1000 + … is what is called a standard geometric series, and the proof says that it is a standard result that the sum of such a series as 1⁄9 (See Appendix: Geometric Series).
- The proof continues: Since, even if there is overlapping, the sum of the segments cannot be greater than 1⁄9 , and that since that is less than the total length of the line segment from 0 to 1 (which is a length of 1), then we cannot actually have included all the real numbers in the line segments that we used.
- Therefore, the ‘proof’ continues, the original supposition that could be a complete listing of the real numbers must have been incorrect, and there cannot be a listing of all the real numbers. Because of that, there must be more real numbers than natural numbers.
It’s almost embarrassingly easy to show that this argument results in a contradiction, which shows that it cannot possibly be correct. What Courant and Robbins have done here is to make an assumption (that there exists a list of real numbers), and then introduce an infinite unending process which includes concomitant assumptions that Courant and Robbins blithely ignore. Then they produce a contradictory result.
At that point they make a classic error of logic. They assume, without providing any logically reasoned argument, that the only possible cause of the contradiction is that some real numbers are not included in the list of real numbers (whatever list might be used). But that:
- does not prove that such numbers cannot possibly be covered by some interval that is centered on a number in the list,
and - does not prove that a collection of such numbers - each of which is a single isolated point - can constitute a length.
It is well known that the rational numbers (numbers that are fractions) between 0 and 1 can be listed (See Appendix: Listing the rational numbers and One-to-one correspondences). They can be set in a list so that for any natural number, there is a corresponding fraction between 0 and 1, and every rational number between 0 and 1 is included in this list. Since that is the case, we can apply the same argument as in the proof above to the fractions between 0 and 1.
And by the argument of the proof, the conclusion is, similarly, that since the list includes every fraction between 0 and 1, then we know that every fraction must be enclosed by one of these line segments 1⁄10, 1⁄100, 1⁄1000 … etc, regardless of how small that segment may be. And, again, according to the argument of the proof, the sum of these line segments cannot be more than 1⁄9 , whereas the entire line segment between 0 and 1 is a length of 1. That means that there must be some remaining part of the line that isn’t made up of any combination of any of the line segments 1⁄10, 1⁄100, 1⁄1000 … .
But there are only two ways there could be points remaining - as non-zero line segments and/or as single points. However, there can’t be any line segments remaining - if we suppose that there could be one such line segment, then there has to be a real number at each end of the line segment, and between any two real numbers, there must always be at least one fraction in that line segment - in fact, there will be limitlessly many fractions in that line segment. That leaves the possibility of single points - but then that would require that a collection of single points, each of which has a length of zero, and none of which taken together can constitute a non-zero interval of the real number line, somehow has a collective length that is greater than zero.
An absurd contradiction
Furthermore, between each such single point there must be an interval (of non-zero width) to either side of it. And every such interval must be made up by intervals from the sequence 1⁄10, 1⁄100, 1⁄1000 … . Hence for every such single point, there is a corresponding non-zero interval to the right side of it, and obviously, every such interval is wider than its endpoints.
But, according to Courant and Robbins, the total width of the interval between zero and 1 is 1, while the total width of these non-zero intervals cannot be more than 1⁄9 which implies that the remaining single points must account for a length of at least 8⁄9 . In other words, according to Courant and Robbins, all these single endpoints taken together are at least 8 times as wide as the intervals for which they are endpoints.
This is completely absurd.
This ridiculous notion is essentially what the axioms of Lebesgue measure theory asks you to accept, see the page Lebesgue measure theory. But even the abstruse machinations of Lebesgue measure theory cannot rescue Courant and Robbins.
So, we now have a contradiction, which I will call the ‘Courant & Robbins contradiction’. Here we do not euphemistically call it a paradox, and by so doing, imply that there just appears to be a contradiction – there is a genuine contradiction here which cannot be brushed aside.
Courant & Robbins claim that there are still points not covered by any interval, and moreover that the length of that collection of points is 8⁄9 . And they claim that there are always points not covered, regardless of the choice of size of the line segments - as long as the initial fraction is less than 1⁄2 (for example, one could choose 1⁄3 or 1⁄57 instead of 1⁄10). Furthermore, they even claim that by choosing a smaller and smaller initial fraction, the total length of the purported single points remaining becomes closer and closer to 1 !
What Courant & Robbins fail to mention is what happens if one scales the whole interval 0 to 1 by some factor. Suppose, for example, that we multiply everything by 1,000,000. The interval 0 to 1 becomes the interval 0 to 1,000,000. Every point in the interval 0 to 1 is multiplied by 1,000,000 - so every point in the interval 0 to 1 has one (and only one) corresponding point in the interval 0 to 1,000,000. This means that for every single point that is not covered over the interval 0 to 1, there is a corresponding point not covered in the interval 0 to 1,000,000, and vice-versa. And this means that we would expect that the calculation of the total length of these uncovered points over the interval 0 to 1,000, 000 should be exactly the same as for the interval 0 to 1. But according to the Courant & Robbins method, these points have a measure of at least 8,000,000⁄9 , that is, at least 888,888 rather than 8⁄9 . This means that you are invited to believe that these uncovered points are somehow magically 1,000,000 times wider than the corresponding uncovered points of the interval 0 to 1. We now have not just one, but two absurd contradictions.
When we have a contradiction, that means that the argument is flawed, and that at least one step in the argument must be rejected as incorrect. So what is going on? Where is the flawed step in the argument?
 The Platonist view assumes that all real numbers are some sort of ‘actual’ things that ‘exist’ in some sense in some ‘reality’, and that they exist simultaneously in this ‘reality’ - and that between any two points there ‘exists’ a section of a line that consists of a limitlessness quantity of points, and that all those points simultaneously ‘exist’ in some sense as ‘actual’ things. The Platonist also assumes that every line segment of real numbers ‘exists’ in this ‘reality’, and all of these line segments ‘exist’ simultaneously. So, accordingly, from the Platonist viewpoint, in the Courant & Robbins contradiction, all the line segments 1⁄10, 1⁄100, 1⁄1000 … ‘exist’, and all ‘exist’ simultaneously. And the sum of all of these line segments also ‘exists’ and is 1⁄9.
The Platonist view assumes that all real numbers are some sort of ‘actual’ things that ‘exist’ in some sense in some ‘reality’, and that they exist simultaneously in this ‘reality’ - and that between any two points there ‘exists’ a section of a line that consists of a limitlessness quantity of points, and that all those points simultaneously ‘exist’ in some sense as ‘actual’ things. The Platonist also assumes that every line segment of real numbers ‘exists’ in this ‘reality’, and all of these line segments ‘exist’ simultaneously. So, accordingly, from the Platonist viewpoint, in the Courant & Robbins contradiction, all the line segments 1⁄10, 1⁄100, 1⁄1000 … ‘exist’, and all ‘exist’ simultaneously. And the sum of all of these line segments also ‘exists’ and is 1⁄9.
A Limitless Series of Segments
But if you are not a Platonist there is no contradiction, and the notion of a ‘sum’ of a limitless quantity of line segments simply doesn’t arise. To see the reason why there is no contradiction for the non-Platonist, consider the Courant & Robbins argument:
1⁄10 = 1⁄10
1⁄10 + 1⁄100 = 11⁄100
1⁄10 + 1⁄100 + 1⁄1000 = 111⁄1000
1⁄10 + 1⁄100 + 1⁄1000 + 1⁄10000 = 1111⁄10000
1⁄10 + 1⁄100 + 1⁄1000 + 1⁄10000 + 1⁄100000 = 11111⁄100000
We see the pattern quite easily, which is
1⁄10, 11⁄100, 111⁄1000, 11111⁄10000, 11111⁄100000, 111111⁄1000000 …
And similarly, when we try to divide 1 by 9 on a calculator, we get 0.1111111111111111. On your calculator, depending on the display panel or how it operates, you might get a different quantity of 1’s. And if you did the calculation by hand, you can add more and more 1’s the longer you calculate for. Theoretically, there is no limit to the quantity of 1’s you could calculate; but one thing is for sure – you will never calculate more than a finite quantity of 1’s.
Limiting Values
If we look at the pattern that is:
1⁄10, 11⁄100, 111⁄1000, 11111⁄10000, 11111⁄100000, 111111⁄1000000 …
it leads us to suspect that these values are all approaching a value of 1⁄9 . This can be confirmed by a formula given by commonly accepted mathematical logic (See Appendix: Geometric Series) but we would be careful to note 1⁄9 is a limiting value that the values never actually reach. The formula does not give the value of the sum of a limitless sum of fractions.
It might be worth pointing out here that, generally speaking, mathematicians aren’t very rigorous when they talk about things that involve limitlessness. Often we see ‘numbers’ written as a sequence of decimal digits with three dots at the end, like this, 0.21382349… The three dots at the end are subject to various interpretations. When it is said, for example, that 0.1326472… is a number, where the … signifies continuing into infinity, in fact this not signify any particular number. What it does actually signify is a set of real number values that lie between the values 0.1326472 and 0.1326473. Often mathematicians will talk about the ‘sum’ of an infinite series of fractions, when what they actually are referring to is not to an actual sum of an infinite quantity of fractions, but to a limit – a limit that cannot be exceeded by the sum of any finite series of fractions. In most cases, the distinction doesn’t matter, but sometimes it does.
When it comes to the notion (as in the Courant & Robbins proof) that we form a one-to-one correspondence of every line segment to a fraction, what this notion actually involves is a definition which simply defines limitlessly many single correspondences, and there is no limit to the quantity of such correspondences. This definition does not require the ‘existence’ of limitless quantities of fractions or of line segments; it is simply a valid logical definition, and it has no dependence on any Platonist beliefs. So when the Courant & Robbins contradiction states that the sum of a limitless quantity of fractions of the form 1⁄10 + 1⁄100 + 1⁄1000 + 1⁄10000 + 1⁄100000 + … is 1⁄9 , the response of a non-Platonist is that that is incorrect. He has no need of any notion such as the sum of a limitless quantity of fractions. For the non-Platonist, there isn’t any contradiction at all in the increasingly smaller line segments scenario. He doesn’t need to believe that these line segments actually exist in some ‘reality’, and he doesn’t need to believe that a sum of all a limitless quantity of line segments ‘exists’. All he does is to observe that the only statements that he can make about these line segments are logical statements regarding the definitions involved, some of which involve limitlessness. And he observes that the process of continually making further line segments never actually finishes, and so a point is never reached where there is a contradiction. For the non-Platonist, the limit of the sums of such fractions as 1⁄10 + 1⁄100 + 1⁄1000 + 1⁄10000 + 1⁄100000 + … is 1⁄9 , but he also acknowledges that that limit is never actually reached. Historically, there have been intense arguments about whether a limitlessness could be considered as completed, see Actual, Completed and Potential Infinity.
So, for the non-Platonist, the refusal to assume that an infinite sum ‘exists’ leads to a resolution of the Courant and Robbins contradiction. The non-Platonist accepts that to deal with an unending process, one must apply limiting values. And the non-Platonist accepts that one can have two different limiting conditions. One can have a limiting value for set membership - the limiting set of all points covered by the intervals; and one can have a limiting value for the sum of ever-decreasing intervals. They are two different limiting values, and one does not necessarily imply the other, since the limit concept is being applied to different aspects of the unending process.
But while the Courant & Robbins contradiction isn’t a contradiction for the non-Platonist, and doesn’t present any difficulties for the non-Platonist, for the Platonist it is an entirely different matter. He cannot state that the sum of a limitless quantity of mathematical entities does not ‘exist’ – because it is a cornerstone of Platonist philosophy that sums of limitless quantities of mathematical entities do ‘exist’, and moreover, that they ‘exist’ independently of any human definition. For example Platonists believe that there are real numbers that are the sum of a limitless number of fractions and which can never be defined by any finite means – and that means that they can only ‘exist’ as ‘actual’ Platonist things. So, from the point of view of the Platonist:
- a limitless quantity of line segments such as 1⁄10, 1⁄100, 1⁄1000, 1⁄10000 … actually ‘exists’, and
- the sum of such a limitless quantity of line segments ‘exists’ and the value of that sum is 1⁄9 , and
- the pairing of every rational number (between 0 and 1) and some line segment such as 1⁄10, 1⁄100, 1⁄1000, 1⁄10000 … ‘exists’,
and the combination of these beliefs results in a contradiction.
A line segment is simply a part of a line that defines a set of all numbers greater than (or greater than or equal to) a given value and less than (or less than or equal to) a given value, so, since the Platonist insists that the sum of an infinite quantity of fractions does ‘exist’, he cannot logically argue that such line segments don’t ‘exist’. Similarly, it would be absurd for a Platonist to argue that while the sum of an infinite quantity of fractions does ‘exist’, the sum of an infinite quantity of line segments cannot ‘exist’.
Different orders of summation
The assertion that the set of covered rationals has a width of 1⁄9 is obtained by taking the simple specific case of adding intervals that are each adjacent to each other and not overlapping , such as the case where one has an interval 0 to 1⁄10 , then and adjacent interval 1⁄10 to 11⁄100 , then another adjacent interval 11⁄100 to 111⁄1000 , and so on, where the intervals converge towards one single limiting point, and where that the limit is given as 1⁄9 - and then simply assuming this applies to the Courant and Robbins case. But the Courant and Robbins case is completely different. Unlike the simple case where the intervals stack nicely against each other, the intervals always zig-zag across the line from 0 to 1, and they can never converge to a single point. The failure to take this into account may be that part of the reason that some people have difficulty with this matter - since besides the fact that for any finite
It is well known that for an infinite series that has both positive and negative terms, the limiting sum is dependent both on the values and the order in which they appear in the series (see Sums of infinitely many fractions: 1). The simplistic summation of infinitely many interval lengths overlooks the crucially important fact that, in the application of a limit, there is no particular order of incrementation of intervals. That is, for any point that might not be covered by an interval, that point can only be obtained by a limit, and for multiple such points, it is not the case that a limit is “reached” for one point, and then, subsequently, a limit is “reached” for another point, and then another.
No - when we apply a limit state to this scenario, there is no particular order of “reaching” the limiting points, and hence there is no particular order of summation and subtraction of the endpoints, and hence the simplistic case does not apply. The naive assumption that one can always calculate the size of such a set by simply adding the lengths, as for a simplistic case, has no logical basis.
The Contradictions of Platonism
The Courant & Robbins contradiction is a compelling argument against Platonism in mathematics. It demonstrates that the Platonist assumption that an actual sum of a limitless quantity of fractions such as 1⁄10 + 1⁄100 + 1⁄1000 + … ‘exists’, and is the same ‘actual’ thing as the value we refer to as 1⁄9 , is logically untenable.
For the non-Platonist, every one of these fractions 1⁄10, 1⁄100, 1⁄1000, 1⁄10000 … is a finite size, however small it may be; and all the fractions are interrelated, since every fraction is 1⁄10 of a previous fraction. And every fraction is related to the first fraction, which is 1⁄10 by being multiplied by 1⁄10 a finite number of times, that is, every such fraction can be expressed as (1⁄10)n where n is some natural number. That means that all such fractions, by the very definition of the series, are of finite size; there cannot be any one of these fractions that is not a definite determined size. But the Platonist view that all such fractions ‘exist’ requires that there ‘exists’ more than a finite quantity of such fractions – and that requires that there must be fractions that are related to the first fraction (which is 1⁄10) by being multiplied by 1⁄10 a limitless number of times. But the Platonist cannot give any value for 1⁄10 multiplied by itself a limitless number of times. He cannot give it any finite value, and neither can he give it a value of zero – because, according to the Platonist creed, there ‘exist’ in some reality, limitlessly many such fractions which consist of 1⁄10 multiplied by itself a limitless number of times, so they can’t all be the value of zero. Of course, the non-Platonist can say that the limiting value as you repeatedly multiply 1⁄10 by 1⁄10 over and over again is zero, that is, the value of (1⁄10)n approaches zero as the value of n gets bigger and bigger – but it never reaches that value. But that is of no help to the Platonist when faced with the Courant & Robbins contradiction. He has no way of circumventing the absurdity of the Platonist viewpoint that the sum of more than a finite quantity of such fractions ‘exists’.
The Platonist claims regarding “actual” infinite sets of numbers is closely related to the notion in one dimension that a line is actually composed of infinitely many points that simultaneously “exist”, which implies the “existence” of adjacent points, a notion that began with Cantor’s ideas of simultaneous “existence” of infinitely many entities. See Cantor’s Grundlagen, Section 1 where he talks about the “actual-infinite”; David Hilbert eulogized Cantor’s notion of two different types of infinity, a “potential infinity” and an “actual infinity”, see David Hilbert on Potential and Actual Infinity.
And more …
For more demonstrations of contradictions arising from the Platonist beliefs in the ‘existence’ of ‘actual’ infinite sets, see Sums of infinitely many fractions: 1 and Sums of infinitely many fractions: 2.
The page Understanding sets of decreasing intervals explains why such definitions of ever-decreasing intervals are inherently contradictory unless they include limiting conditions, and the page Lebesgue measure theory demonstrates in more detail why the conventional assumption that you can add the lengths of infinitely many intervals as an infinite sum such as 1⁄10 + 1⁄100 + 1⁄1000 + … is naive and simplistic, and overlooks crucial details.
You can also see a formal paper on some of the problems of calculating the total measure of some sets that are defined in terms of limitlessness, see PDF On Smith-Volterra-Cantor sets and their measure.
For more on Platonism see Platonism, The Myths of Platonism and Platonism’s Logical Blunder, Numbers, chairs and unicorns and the posts Moderate Platonism and Descartes’ Platonism.
Appendix: Geometric Series
For a limitlessly long geometric series in the form of
![]()
the sum of the first n + 1 terms is:
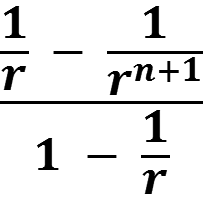
Provided the value of r is greater than 1, then the value of ![]() decreases as n increases, and the limiting value of
decreases as n increases, and the limiting value of ![]() as n increases is zero.
as n increases is zero.
That gives the standard result that the limiting value of the sum as n increases, provided r is greater than 1 is:
![]() which is the same as
which is the same as ![]()
For the series 1⁄10 + 1⁄100 + 1⁄1000 + 1⁄10000 + 1⁄100000 … r is 10, and so the limit of the sum as n increases is given as
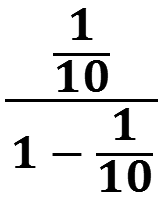
which evaluates as 1⁄9 . And that means that, no matter how many terms are in the series, the value of the series can never exceed the value 1⁄9 . To put it another way, the limiting value that any such sum of a finite quantity of terms approaches, but never actually reaches, is 1⁄9 . Note that the quantity
![]()
in the formula can never actually be zero; every fraction that is in the series is of the form
![]()
where y is always some finite number. There is no fraction in the series where y is not some finite number.
Note that 0.999… is usually used to indicate the limiting value of the series:
9⁄10 + 9⁄100 + 9⁄1000 + 9⁄10000 + 9⁄100000 …
Since this is the same as 9 × (1⁄10 + 1⁄100 + 1⁄1000 + 1⁄10000 + 1⁄100000 …), then the limiting value is 9 × 1⁄9 , which is 1.
Appendix: Listing the rational numbers
There is more than one way of making a list (an enumeration) of the rational numbers. An easy way is to visualize a method, by using horizontal rows, the first with all fractions with 1 on the top, the next row with all the fractions with 2 on the top, and so on, like this:

Then we can envisage a simple way of progressing through the fractions so as to not miss any on the way. We can do this by taking each column in turn, like this:

This scheme outlines a way of listing all the positive rational numbers. Although it is a visual scheme, there is no reason why the methodology could not be defined without using any visual cues. Of course, the list never finishes, and that is because there is no limit to the quantity of rational numbers. You might notice that in this scheme some numbers are repeated, since 1⁄1 = 2⁄2 , and 2⁄1 = 4⁄2 . This is true, but the important point is that the scheme doesn’t omit any rational numbers. And if you wanted to include negative numbers, then you do the same scheme except that you simply include a negative of each number immediately after each number.
If you want to list only the fractions between say, 0 and 1, then you simply leave out the fractions that are greater than one, like this:
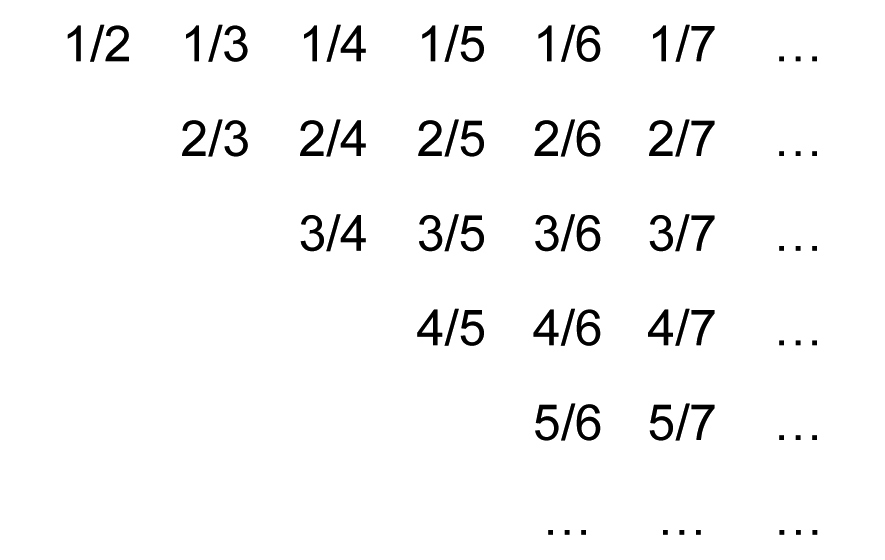
and make a list in the same way as before. See also A specific listing of rational numbers.


Rationale: Every logical argument must be defined in some language, and every language has limitations. Attempting to construct a logical argument while ignoring how the limitations of language might affect that argument is a bizarre approach. The correct acknowledgment of the interactions of logic and language explains almost all of the paradoxes, and resolves almost all of the contradictions, conundrums, and contentious issues in modern philosophy and mathematics.
Site Mission
Please see the menu for numerous articles of interest. Please leave a comment or send an email if you are interested in the material on this site.
Interested in supporting this site?
You can help by sharing the site with others. You can also donate at where there are full details.
where there are full details.