Alexander’s Horned Sphere
Page last updated 29 June 2022
Note: Since this page was first written, a David Pierce has written an article that references it; I address that in Alexander’s Sphere and Impossible Objects.
The Alexander Horned Sphere isn’t really a sphere at all - in fact, there isn’t any physical thing that is an Alexander Horned Sphere. It’s just a hypothetical notion. The notion revolves around the idea that you start off with a stretchy rubber-like sphere that you can stretch and bend and squeeze any way you like. You then shape it so that it is like a solid torus (the shape of a standard finger ring) but with a bit cut out if it, like in this picture:
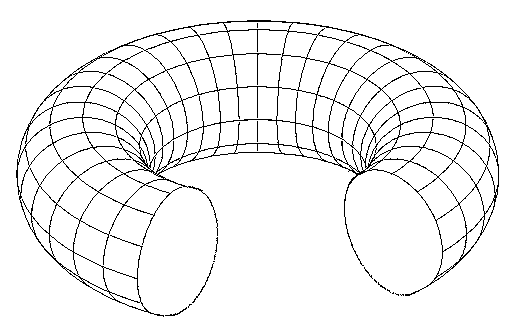
Now, you add to each cut end, two arms that almost but don’t quite touch together. And there’s an important bit here. The arms from either end of the cut go around each other, but since the arms don’t touch together, and since the whole thing is completely elastic, you can still separate the arms, and so by a bit a judicious squeezing and stretching, you can still return it to its original shape (as in the above picture).
The Horned Sphere notion is “defined” as the result of doing this adding of quasi-interlinked arms to each existing arm end infinitely many times. And this is where the problems arise. By vaguely stating that the process is continued infinitely many times, you aren’t making a clear definition at all. This is because, for this process, the continuation of the process never finishes, regardless of how many times it is repeated. And if all you have is a vague definition that talks about repeating the process infinitely many times, then you don’t have a clear definition of anything at all. Since the repetition never completes, then since the object is perfectly squeezable, then it must always be possible to separate the quasi-interlinked arms and return to the original shape. The picture below gives an idea of what is happening.
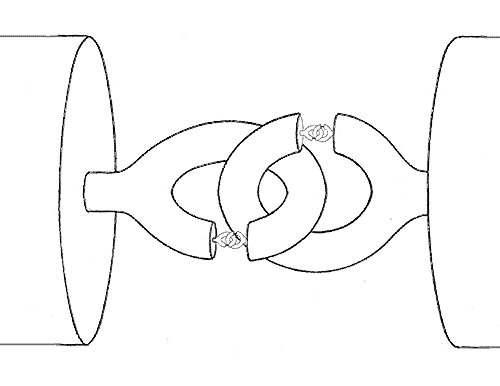
Given the “definition” of the horned sphere, analyzing what is actually happening is complicated by the fact that at each repetition, more arms appear, and the object becomes increasingly hard to visualize. But we can concentrate on what is happening by ensuring that the number of arms does not increase at each repetition. This gives us a situation somewhat like the picture below:
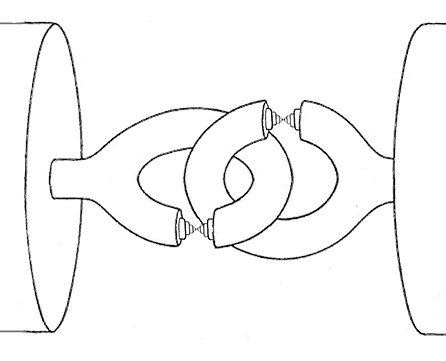
Clarification by Limits
Now it is easy to see that as the added arms get smaller and smaller, it might be possible to define a limiting case where the arms converge to a single point. Now, if the definition is such that this single point is the same for both ends of the left arms, and similarly for both ends of the right arms, and if the definition is that there is no break between these single points and the defined arms, then, clearly, the arms are properly interlinked, and cannot be separated by any amount of squeezing or reshaping.
And if the limiting case for the infinite repetition is that the limit points for the left arms and the right arms are separated, then the arms are not fully interlinked, and can be separated by a bit of squeezing and reshaping.
The only difference for the case where the number of arms increases at each repetition is that there is then infinitely many limiting points. But the question of whether the arms are inseparably linked or not is only dependent on whether each limit point of the left arms coincides with the corresponding limit point of the right arms.
And that’s all there is to the Alexander horned sphere. There’s nothing difficult or strange about it at all if you analyze it logically. Since writing this page, I noticed that a David Pierce has written an article about the Alexander sphere where he questions my understanding of the matter, and so I have created another webpage Alexander’s Sphere and Impossible Objects, which discusses in detail Pierce’s article.


Rationale: Every logical argument must be defined in some language, and every language has limitations. Attempting to construct a logical argument while ignoring how the limitations of language might affect that argument is a bizarre approach. The correct acknowledgment of the interactions of logic and language explains almost all of the paradoxes, and resolves almost all of the contradictions, conundrums, and contentious issues in modern philosophy and mathematics.
Site Mission
Please see the menu for numerous articles of interest. Please leave a comment or send an email if you are interested in the material on this site.
Interested in supporting this site?
You can help by sharing the site with others. You can also donate at where there are full details.
where there are full details.