Cantor’s Grundlagen
“Grundlagen einer allgemeinen Mannigfaltigkeits­lehre”
(Foundations of a general theory of sets)
• English Translation •

This is a new (2021) English translation of Cantor’s Grundlagen einer allgemeinen Mannigfaltigkeitslehre. Ein mathematisch-philosophischer Versuch in der Lehre des Unendlichen (Foundations of a general theory of sets: A mathematical-philosophical investigation into the theory of the infinite), which is the fifth part of his work Über unendliche lineare Punktmannig-faltigkeiten. Also available online are English translations of Part 1, Part 2 and Part 3. (Footnote: Translator’s note: As published by Teubner, Leipzig 1883. This is the fifth part of a series of papers by Cantor coming under the overall title of Über unendliche lineare Punktmannig-faltigkeiten (On infinite linear point-sets), which were published in the Mathematische Annalen between 1879 and 1884:
Part 1. Mathematische Annalen 15, 1879, pp. 1-7
Part 2. Mathematische Annalen 17, 1880, pp. 355-358
Part 3. Mathematische Annalen 20, 1882, pp. 113-121
Part 4. Mathematische Annalen 21, 1883, pp. 51-58
Part 5. (Grundlagen) Mathematische Annalen 21, 1883, pp. 545-591
Part 6. Mathematische Annalen 23, 1884, pp. 453-488
This translation uses a 1984 Springer reprint of the above collection, which uses a later published edition which includes a subtitle, a preface, and some footnotes to the original, e-ISBN-13:978-3-7091-9516.1, DOl: 10.1007/978-3-7091-9516-1. ) This translation uses current terminology if possible where the older terminology might cause confusion for modern readers.

English translation by James R Meyer, copyright 2021 www.jamesrmeyer.com

Notes: For convenience I have added descriptive titles to the sections, these are in green italics enclosed by square parentheses, e.g. [The infinite]. The footnotes are Cantor’s, unless in green text and indicated by “Translator’s note:”.

INDEX

PREFACE

This treatise will appear shortly in Mathematische Annalen as the fifth issue of an article entitled “Infinite Linear Point-Manifolds”; the first four are contained in volumes 15, 17, 20 and 21 of the same magazine. All of these works are linked to two articles I published (Crelle’s Journal, Vols. 77 and 84), in which the main ideas that guided me in the theory of sets are already there. Since the present essay takes the subject much further, and from its main thesis is independent of the previous articles, I decided to publish it separately below a title that most closely matches its content.

As I issue these pages to the public, I must note that I wrote them with two kinds of readers in mind, for the philosophers who have followed the developments in mathematics up to the most recent of times, and for mathematicians who are versed in the most important results, ancient and modern, of philosophy.

I know very well that the subject that I am talking about has always given rise to the most diverse opinions and concepts, and that neither the mathematicians nor the philosophers have reached agreement on all points. So I do not think that, in a matter as difficult, complicated and all-encompassing as infinity, I must have said the last word. But since after many years of research on this subject I have come to final convictions, and since, in the course of my studies, these beliefs have not wavered but have only become more strengthened, I considered that I had an obligation to put them in order and make them known.

May I therefore have discovered and expressed the objective truth that I have endeavored to determine.

Halle, Christmas 1882

§ 1 [The infinite]

The previous accounts of my investigations in the theory of sets (Footnote: Theory of sets. With this term I designate a very comprehensive theoretical term that I have so far only tried to develop in the specific design of arithmetical or geometrical set theory. By a manifold or set, I generally understand every multiple that can be thought of as one, i.e: every set of certain elements, which can be connected into a whole by a rule. I believe that I am defining something that is related to the Platonist idea, as well as to what Plato in his dialogues “Philebos or the highest good”. He sets this against the unlimited, the indefinite, which I call the non-actual-infinite, as well as the limit and explains it as an ordered “mixture” of the latter two terms. Plato himself suggested that the terms are of Pythagorean origin (see A. Boeckh, Philolaos des Pythagoreers Lehren, Berlin 1819).) has reached a point where its continuation depends on extending the notion of actual integers beyond the previous limits, and this extension lies in a direction that, as far as I know, no-one has previously sought to tread.

Without this expansion of the concept of number, I would be so constrained that it would hardly be possible for me to take the smallest step further forward in set theory. It might be considered that this dependency on such an expansion is a justification, or perhaps an excuse, for the fact that I introduce seemingly alien ideas into my work, because it involves an extension, a continuation of the sequence of numbers beyond the infinite. And however daring this may seem, I nevertheless express not only the hope, but the firm conviction that this extension will over time be regarded as completely simple, correct and natural. In doing so, I am under no illusion that with this enterprise I am placing myself in opposition to widespread intuitions regarding the mathematical infinite and commonly held opinions regarding the quantity of numbers.

As for the mathematical infinite, insofar as it has found a justifiable application in science and contributed to its usefulness, it appears to me that up to now it has appeared mainly in the role of a variable quantity, which either grows beyond all limits or is diminished to any desired diminutiveness, but always remains finite. I call this infinite the non-actual-infinite.

However, in more recent times, in geometry and in the theory of functions, another equally justifiable concept of the infinite has been developed, where, for example, in the investigation of an analytic function of a complex variable, it becomes necessary and commonly accepted, to conceive of a single point that lies at infinity (i.e: an infinitely distant but definitive point) in the plane of the complex variables, and to examine the behavior of the function in the vicinity of that point, just as in the vicinity of any other point. It turns out that the function shows exactly the same behavior in the vicinity of the infinitely distant point as at any other finitely distant point, so that in this case we are fully justified in thinking of the infinite as placed at a completely specific point.

When the infinite appears in such a definitive form I call it the actual-infinite.

The emergence of these two manifestations of the mathematical infinite has led to great advances in geometry, in analysis, and in mathematical physics, and we will maintain a distinction between them in order to understand the following.

The first form, the non-actual-infinite, occurs as a variable finite, while the other form, the actual-infinite, as I call it, appears as a completely determinate infinite. The notion of actual-infinite integers (which I will define later) was with me for many years before I realized that they are concrete numbers of real significance. (Footnote: Previously I called them “definitively defined infinity symbols”; see Mathematische Annalen, Vol. 17, p. 357; Vol. 20, p. 113; Vol. 21, p. 54.) They have absolutely nothing in common with the non-actual-infinite; rather, they have the same property of determinativity that we find in infinitely distant points in the theory of analytic functions, i.e: they belong to the realm of the actual-infinite. But while the point at infinity of the plane of complex numbers is isolated from all points that lie in the finite region, here we have not simply a single infinite integer but an infinite sequence of them, and which are clearly differentiated from each other, and are in accordance with rule-based relations of number theory both among themselves and to finite integers. But these relationships are not such that they allow themselves to be reduced essentially to the relations of finite numbers with each other. These relations in fact appear frequently, but only in the different intensities and forms of the non-actual-infinite, for example, in functions of a variable x that grows infinitely large or infinitely small, where they become certain numbers of finite order as they become infinite. Such relationships in fact can be considered as concealed relations of the finite, or in any case immediately reducible to the finite. On the contrary, the rules for the actual-infinite integers, which will be defined later, are initially different from those that apply in the finite, but this does not exclude the possibility that the finite real numbers themselves can obtain certain new properties with assistance from the actual-infinite numbers.

The two principles of generation by which, as will be shown, the new actual-infinite numbers are defined, are of such a kind that, through their combined application, every limitation in the conception of the formation of actual integers can be overcome. Fortunately, as we shall see, a third principle applies in opposition, which I call the principle of constraint or limitation, by which certain limits are successively imposed on the absolutely endless process of generation, so that we have a natural segmentation of the absolutely infinite sequence of integers, into what I call number-classes.

The first number-class (I) is the set of finite integers 1, 2, 3, …, v, …, which is followed by the second number-class (II), consisting of specific infinite integers following upon one another in a determinate sequence. Once the definition of the second number-class is given, the third follows, and then the fourth, and so on.

The introduction of these new integers seems to me of the greatest significance for the development and advancement of my concept of “cardinal-number” as introduced in the previous parts of this work and elsewhere. (Footnote: Crelle’s Journal, Vol. 77, p. 257 (Translator’s note: See English translation at Cantor’s 1874 Proof of Non-denumerability)
Crelle’s Journal, Vol. 84, p. 242 (Translator’s note: See English translation at A Contribution to the Theory of Sets).) According to this concept, every well-defined set has a determinate cardinal-number; two sets have the same cardinal-number if they can be correlated with one another element for element.

In the case of finite sets, the cardinal-number coincides with the number of elements, since such sets are known to have the same cardinal-number of elements regardless of any ordering.

In the case of infinite sets, on the other hand, no-one has made mention of a precisely defined cardinal-number of their elements, either in my work or anywhere else, but a certain cardinal-number, completely independent of any ordering of their elements, can also be ascribed to them.

The smallest cardinal-number of infinite sets must be ascribed, as is easy to justify, to those sets which can clearly correspond to the first number-class and which therefore have the same cardinal-number as it. On the other hand, an equally simple, natural definition of the higher cardinal-numbers has so far been lacking.

Our above-mentioned number-classes of the actual-infinite integers are now identified as the natural, uniformly presented representatives of the cardinal-numbers of well-defined sets, and which increase according to definite rules. I will show most definitely that the cardinal-number of the second number-class (II) is not only different from the cardinal-number of the first number-class, but that it is actually the next highest cardinal-number, and consequently we can call it the second cardinal-number or the cardinal-number of the second number-class. Likewise, the third number-class gives the definition of the third cardinal-number, the cardinal-number of the third number-class and so on and so on.

§ 2 [Ordering and well-ordered sets]

Another great gain that can be attributed to the new numbers consists for me in a new concept, unmentioned previously by anyone else, regarding the “ordinal-number” of elements of a well-ordered infinite set. Since this concept is always expressed by a very specific number in our expanded number realm, provided that the order of the elements of the set (which will shortly be more fully defined) is determined, and since, on the other hand, the concept of ordinal-number receives a direct objective representation within our inner intuition, then by this connection between the concept of cardinal-numbers and ordinal-numbers, the reality of the latter, which I emphasize, is also demonstrated in cases where they are actual-infinite.

A well-ordered set is to be understood as any well-defined set in which the elements are connected to one another by a certain determinate ordering, according to which there is a first element of the set, and where each individual element (if it is not the last in the ordering) is followed by another, and similarly for any finite or infinite set of elements, there is a definite element which is the immediate successor in the ordering (unless there is nothing following the totality of ordering). Two “well-ordered” sets are said to be of the same ordinal-number (with reference to their given orderings) if a mutually unambiguous correspondence of them is possible in such a way that if E and F are any two elements of one, and E₁ and F₁ the corresponding elements of the other, the position of E and F in the ordering of the first set is always in agreement with the position of E₁ and F₁ in the ordering of the second set, so that if E precedes F in the ordering of the first set, then E₁ also precedes F₁ in the ordering of the second set. This correspondence, if it is actually possible, as can easily be seen, is always completely determinate. And since there is always one and only one number α in the extended sequence of numbers, where the numbers preceding it (from 1 onwards) have the same ordinal-number in the natural ordering, it is necessary that the ordinal-number of both of those “well-ordered” sets is exactly equal to α, if α is an infinitely large number, and equal to the number α -1 which precedes the number α, if α is a finite integer.

The essential difference between finite and infinite sets is shown by the fact that a finite set, for every ordering that can be applied given to its elements, presents the same ordinal-number of elements. On the other hand, a set consisting of an infinite number of elements will in general be assigned different ordinal-numbers, according to the ordering that is applied to the elements. As we have seen, the cardinal-number of a set is a property of that set, independent of its ordering, but as soon as one has to deal with infinite sets, the ordinal-number of a set is evidently a factor that in general is dependent on a given ordering of its elements. Nevertheless, even in the case of infinite sets, there is a certain correlation between the cardinal-number of the set and the ordinal-number of its elements that is determined for a given ordering.

If we first take a set that has the cardinal-number of the first class and give the elements any specific ordering so that it becomes a “well-ordered set”, then its ordinal-number is always a specific number of the second number-class and can never be replaced by any other number of any other number-class. On the other hand, any set of the first cardinal-number can be given an ordering so that its ordinal-number, with reference to this ordering, becomes equal to any selected number of the second number-class. We can also express this in the following way: every set of the cardinal-number of the first number-class can be counted by numbers of the second number-class and only by such numbers, and indeed the set can always be given such an ordering of its elements that it can be counted in this ordering by any given number of the second number-class, and that number indicates the ordinal-number of elements of the set with reference to that ordering.

Analogous rules apply for the sets of higher infinite cardinal-numbers. Hence every well-defined set with the cardinal-number of the second number-class is countable by numbers of the third number-class and only by such numbers, and indeed the set can always be given such an ordering of its elements that it can be countable (Footnote: What I have previously called “countable” in the earlier numbers of this work is, according to the definition now introduced (tightened and generalized) nothing more than the countability by numbers of the first number-class (sets of finite numbers) or by numbers of the second number-class (sets of transfinite numbers). ) in this ordering by an arbitrarily specified number of the third number-class, and this number determines the ordinal-number of elements of the set with reference to that ordering.

§ 3 [Rules concerning ordering]

The concept of the well-ordered set proves to be fundamental for the whole theory of sets. It is always possible to bring any well-defined set into the form of a well-ordered set. I shall come back to this law of thought, which seems to me to be fundamental and momentous, and which is particularly remarkable due to its universality. Here I limit myself to the demonstration of how the basic operations for the integers, whether they are finite or actual-infinite numbers, result in the simplest way from the concept of the well-ordered set, and how the rules for these derive immediately with absolute certainty from inner intuition. If two well-ordered sets M and M₁ are given, to which the ordinal-numbers correspond as numbers α and β, then M + M₁ is also a well-ordered set, which arises when the first set M followed by the set M₁ and is and united with it; a certain ordinal-number corresponds to this set M + M₁ in respect of the resulting ordering of its elements. If α and β are not both finite, then α and β is generally different from β and α. The commutative rule ceases to be generally valid even for addition. It is now easy to form the concept of the sum of several summands given in a certain sequence, whereby this sequence itself can be actual-infinite, so that I do not need go into more detail at this point. I therefore only note that the associative rule generally proves to be valid, specifically: α + (β + γ) = (α + β) + γ

If one takes a succession, determined by a number β, of similar sets which are similarly ordered, in which the ordinal-number of elements is each equal to α, then one obtains a well-ordered set, the corresponding ordinal-number of which gives the definition for the product β α, where β is the multiplier, and α is the multiplicand; here, too, it is found that β α generally differs from α β, that is, the commutative rule is generally invalid for the multiplication of numbers. On the other hand, one finds that the associative rule also applies in multiplication, so that one has: α (β γ) = (α β) γ.

Of the new numbers, certain of them are distinguished from the others by the fact that they have a prime number property, but this must be characterized here in a somewhat more specific way by understanding a number α where the decomposition α = β γ (where the multiplier is β ) is not possible unless β = 1 or β = α. On the other hand, in general, even with prime numbers where α is the multiplicand, there will be a certain margin of indeterminacy, and it is in the nature of things that this cannot be resolved. Nonetheless, in a later paper it will be shown that the factoring of a number into its prime factors can always be done in an essentially unique manner, even with regard to the sequence of the factors (as long as they are not finite prime numbers that occur adjacent in the product). Two types of actual-infinite prime numbers emerge, of which the first type is closer to the finite prime numbers, whereas the prime numbers of the second type have a completely different character.

Furthermore, with the help of the new knowledge, I will soon be able to provide a strict justification for the proposition regarding the so-called linear infinite sets that is cited at the end of my article Ein Beitrag zur Mannigfaltigkeitslehre. (Footnote: Ein Beitrag zur Mannigfaltigkeitslehre, Crelle’s Journal, 1878, Vol. 84, p. 257.
Translator’s note, see an online English translation of that article at A Contribution to the Theory of Sets.)

In the previous part of this work (Part 4), (Footnote: Mathematische Annalen, Vol. 21, p. 54 ) I proved a proposition for point-sets P which are continuous in an n-dimensional region, that uses an application of the new, previously defined terminology, which is as follows: (Footnote: Translator’s note: The derivative of a set of points S (a point-set) is defined as the set of all limit points of S, where informally, a limit point of a set S is a point which has points of S, other than itself, arbitrarily close to it. Successive derivation operations can be carried out on the resultant set; Cantor indicates the result of the α^th such operation by P^(α). See Part 1.)

“If a point-set whose derivative P^(α) vanishes identically, where α is any integer of the first or second number-class, then the first derivative P ⁽¹⁾, and therefore also P itself, is a point-set with the cardinal-number of the first number-class.”

It seems to me most remarkable that this proposition can be reversed as follows:

“If P is a point-set whose first derivative P ⁽¹⁾ is the cardinal-number of the first number-class, then there are integers α belonging to the first or second number-class for which P^(α) vanishes identically, and of all such numbers α for which this phenomenon occurs, there exists a smallest such α.”

I shall publish the proof of this theorem in the near future, in response to a kind invitation from my esteemed friend, Herm Prof. Mittag-Leffler in Stockholm, in the first volume of the new mathematical journal (Acta Mathematica) of which he is the editor. Following upon this, Mittag-Leffler will publish an article in which he will show how, on the basis of this theorem, his and Prof. Weierstrass’s investigations into the existence of unambiguous analytic functions with given singularities can be given considerable generalizations.

§ 4 [Extending the current notions of the infinite]

The extended integer sequence can, if required, be easily completed into a continuous set of numbers by adding to every integer α all real numbers x that are greater than zero and less than one.

Since in this way a certain expansion of the domain of the real number into the infinitely large is attained, perhaps a connected question will be whether one could not also with the same success define certain infinitely small numbers, or what might amount to the same thing, finite numbers which do not coincide with the rational and irrational numbers (which appear as limit values of sequences of rational numbers), but could be included into what one assumes are intermediate points in the midst of the real numbers, just like the irrational numbers in the realm of the rational, or like the transcendental numbers into the structure of algebraic numbers?

The question of the production of such interpolations, on which a lot of effort has been applied by some authors, can, in my opinion and as I will show, only be answered clearly and unambiguously with the help of our new numbers and, in particular, on the basis of the general concept of the number of well-ordered sets. Previous attempts, it seems to me, are based partly on an erroneous confusion of the non-actual-infinite with the actual-infinite, and partly on a completely uncertain and fluctuating basis.

The non-actual-infinite has often been called the “bad” infinite by recent philosophers, wrongly in my opinion, since it has proved itself to be a very good, extremely useful instrument in mathematics and in natural knowledge. As far as I know, the infinitely small quantities have so far only been developed for use in the form of the non-actual-infinite, and as such are capable of all those differences, modifications and relationships which are used and expressed in infinitesimal analysis and in the theory of functions, in order to establish the abundance of analytical truths there. On the other hand, all attempts to force this infinitely small into some actual-infinitely small would have to be given up as being pointless. If, otherwise, actual-infinitely small sizes exist, i.e: they are definable, they are certainly not directly related to the usual, infinitely decreasingly small quantities.

In contrast to the aforementioned observations on the infinitely small and the confusion of the two manifestations of the infinite, there is an opinion regarding the essence and meaning of numerical quantities, which is that no numerical quantities are believed to actually exist, apart from the integers of our first number-class (I).

At most, the rational numbers that follow directly from them are granted a certain degree of reality. But as far as the irrationals are concerned, they are assumed to have a purely formal meaning in mathematics, in that they serve to a certain extent only as arithmetical symbols that assign properties of groups of integers and to describe them in a simple, uniform way. According to this viewpoint, the true substance of analysis is formed exclusively from finite integers, and all truths found in arithmetic and analysis or still awaiting discovery are to be understood as relationships of integers to one another. Infinitesimal analysis, and with it the theory of functions, is considered legitimate only to the extent that its terms can be demonstrably interpreted as rules governing integers. With this viewpoint concerning pure mathematics, although I cannot agree with it, there are undoubtedly certain advantages attached to it, which I would like to emphasize here, and its proponents also argue for its importance.

If, as we assume here, only the finite integers are real, but all the rest are nothing other than types of relationships, then it can be required that the proofs of the analytical theorems be checked for their “number-theoretic validity” and that every gap that occurs in them indicates how they must be filled according to the principles of arithmetic. The true touchstone for the legitimacy and perfect certainty of the evidence is seen in the efficiency of such completion. It cannot be denied that in this way this rationalization can be perfected and that it can bring about other improvements in methods in various parts of analysis. By observing the principles emanating from that view one can also see that it is a safeguard against any kind of inconsistencies or mistakes.

In this way a definite, if rather sober and obvious principle is established, and which is recommended to all as a guideline; it should serve to show the trajectory of the mathematical desire to speculate and conceptualize within the true boundaries, and where it avoids the danger of falling into the abyss of the “supernatural”, where, as is said with fear and a healthy concern, “Anything might be possible”. It is left as an open question whether or not it was just an attitude of expediency that led to the authors of this attitude seeing themselves as acting as an effective safeguard regulating the rising forces, which can be so easily led into danger by arrogance and extremism, and as an effective protection against all errors, even if no useful principle can be found in it. That they began with these principles even when they were discovering new truths is an assumption that, for me, is out of the question, because regardless of how many good things I might get from these maxims, I must, strictly speaking, consider them to be erroneous. We do not owe any real progress to them, and if it had actually been the case that they had been followed exactly, then our knowledge would have been held back or at least confined within the narrowest of limits. Fortunately, things are in fact not so bad, and though both the praise and the observance of those rules are useful under certain circumstances, their assumptions have never been taken literally. It is also striking to observe that up to now, there has been a lack of anyone to undertake a formulation more complete and better than has been attempted here by myself.

If we examine history, we see that similar views were often represented and found as early as in Aristotle’s works. It is well known that in the Middle Ages, the “infinitum actu non datur” (the actual-infinite does not exist) was always represented by all scholastics as an irrefutable sentence taken from Aristotle. If, however, one considers the reasons which Aristotle (Footnote: Aristotle: See the presentation of Zeller in his great work, The Philosophy of the Greeks, 3rd Ed., Part II, 2nd section. pp. 393 to 403. Plato’s conception of the infinite is quite different from that of Aristotle; see Zeller Part II, 1st section. pp. 628-646. I also find points of contact for my views in the philosophy of Nicolas of Cusa. See: R. Zimmermann, The Cardinal Nieolaus of Cusa as a predecessor of Leibniz (Sitzungsberichte der Wiener Akademie der Wissenschaften, 1862). I note the same in relation to Giordano Bruno, the successor to Nicolas of Cusa. See Brunnhofer, Giordano Bruno’s Weltansehauung and Verhängnis Leipzig 1882.
An essential difference, however, is that I fix the different degrees of the actual-infinite by the numbers (I), (II), (III) etc. once and for all according to that concept and only then do I consider it a task to consider the relationships between them, not only to investigate the numbers mathematically, but also to determine them and record them wherever they occur in nature. There is no doubt for me that we will continue on this path, never reaching an insurmountable boundary, but also not reaching any sort of comprehension of the absolute. The absolute can only be recognized, but never known, not even approximately known.
For just as for every finite number, no matter how large, there is the same infinite first number-class (I), in the same way every transfinite number, however large, is surmounted by one of the higher cardinal-numbers (II) or (III), and so on, giving us a set of numbers and number-classes, whose cardinal-number is no less than that of the entire set of the absolute infinity of numbers that follow after 1. It is similar to how Albrecht von Haller says of eternity: “I subtract it and You lie right in front of me.”
The absolutely infinite sequence of numbers therefore appears to me in a certain sense as a suitable symbol of the absolute, whereas the infinity of the first number-class (I) previously served only one purpose for me, which was precisely that I considered it to be a tangible notion, rather than just a representation, of how something that completely vanishes to nothing appears in comparison to that infinity.
It also strikes me as remarkable that each of the number-classes, and therefore each of the cardinal-numbers, is assigned to a very specific number of the absolutely infinite total set of numbers, namely in such a way that for every transfinite number γ there is also a cardinal-number which is called the γ^th. The different cardinal-numbers thus also form an absolutely infinite sequence. This is all the more remarkable as the number γ, which indicates the cardinal-number (if there is a number preceding the number γ) of the numbers of that number-class (and which has this cardinal-number), is in a proportion whose smallness defies any description and the more so, the greater that γ is.) gives against the real existence of the infinite (see for example his Metaphysics, Book XI, Chapter 10), then they essentially lead back to one presupposition, involving one petitio principii (begging the question), based on the assumption that there are only finite numbers, which he concluded from the fact that he was only aware of things in finite quantities. I believe, however, to have proved above, and this will be shown even more clearly in the remainder of this work, that definite countings can be made on infinite sets as well as on finite sets, provided that the sets follow a certain rule which is that they can be well-ordered sets. Without such a rule regarding the ordering of the elements of a set no counting can be done on the set - this is in the nature of the concept of counting. Even in the case of finite quantities, a counting can only be carried out for a certain sequence of the counted elements, but here it shows as a special nature of finite quantities that the result of the counting - the ordinal-number - is independent of the respective arrangement; while in the case of infinite quantities, as we have seen, such independence in general does not apply, but the number of an infinite set is an infinite integer which is also determined by the rule of counting. This is where the essential difference between the finite and the infinite lies, which is based upon nature itself and can therefore never be eradicated, but the existence of the infinite will never henceforth be denied on account of this difference, while the existence of the finite must be admitted - if one is permitted to fall, then we have to do away with the other also - if so, where would this road take us?

Another argument used by Aristotle against the reality of the infinite consists in the assertion that the finite, if it existed, would be abolished and destroyed by the infinite, because a finite number is supposedly annihilated by an infinite number. As one will see clearly in the following, in truth the fact is that for an infinite number, if it is considered to be perfectly determined, a finite number can very easily be added and united with it, without eliminating the finite number; the infinite number is modified by the addition of a finite number to it. It is only the reverse process, when the finite number is set first in the addition, that causes the elimination of the finite number without causing any modification of the infinite number. This correct state of the matter with regard to the finite and the infinite, which Aristotle completely misunderstood, could lead to new ideas not only in analysis but also in other sciences, especially in the natural sciences.

While I am interested in the concepts of the infinitely large in the form of increasing without limit and also in the closely related form of the convergent infinite sequences (first introduced in the seventeenth century), but I am also impelled, almost against my will, to perfect the definitive form of the mathematics of infinite numbers. In contrast to traditions that are valuable to me, through the course of many years of scientific endeavors and attempts I have been logically compelled by many years of scientific endeavors and attempts to do so, and because of this, I also believe that no argument can be asserted against them that I would not know how to counter.

§ 5 [The justification for extending the infinite]

When I spoke of traditions, this was not to understand them in the narrow sense of what was experienced, but rather to follow them back to the founders of modern philosophy and natural sciences. In order to assess the question that is at stake here, I cite only a few of the most important sources, such as:

One cannot devise even today any stronger reasons than those noted here against the introduction of infinite integers; one may therefore examine them and compare them with mine. I will reserve a detailed and exhaustive discussion of these passages, and in particular of Spinoza’s most replete and important letter to L. Meyer, for another opportunity, but I will limit myself here to the following.

As different as the theories of these writers are, in their judgment of the finite and the infinite they essentially agree that the concept of a number includes the finiteness of it, and that on the other hand the true infinite or absolute, which resides in God, is not permitted any determination. As far as the latter point is concerned, I fully agree with it, as it cannot be otherwise, because the sentence: “omnis determinatio est negatio” (every determination is negative) is, for me, completely beyond question. On the other hand, as I have already said above when discussing the Aristotelian reasons against the “infinitum actu” (actual-infinite), I see in the former a petitio principii (begging the question), which renders explainable many contradictions which can be found in all these authors and especially in Spinoza and Leibniz. The assumption is that, apart from the finite, and the absolute infinite that cannot be reached by any determination, there can be no new entities which are infinite but at the same time are determinate numbers, the ones that I refer to as the actual-infinite. I do not find that this assumption is justified by anything and, in my opinion, it even stands in contradiction to certain assertions put forward by the two aforementioned philosophers. What I maintain and believe to have proved through this work, as well as through my earlier efforts, is that after the finite there is a transfinite (which might also be called a suprafinite), i.e: it gives an unlimited scale of definitive steps, which in their nature are not finite but rather infinite, but which, like finite entities, can be determined by definite, well-defined and mutually distinguishable numbers. My conviction is therefore that the finite magnitudes do not constrict the realm of definable magnitudes and that the limits of our knowledge can be extended accordingly without our nature having to apply any limitation. Instead of the Aristotelian school sentence discussed above in § 4, I therefore put another:

“Omnia seu finita seu infinita definita sunt et excepto Deo ab intellectu determinari possunt.” (All things finite or infinite are definite and, except for God, can be determined by the intellect). (Footnote: Determinari possunt: I cannot ascribe any being to any indeterminate, changeable, non-actual-infinites, in whatever form they appear, because they are nothing but either relational concepts or purely subjective ideas, respectively. Beliefs and imaginations in any case are not adequate ideas. Hence, if only the non-actual-infinite were meant by the sentence “infinitum actu non datur” (the actual-infinite does not exist), I could subscribe to it, but it would then be a purely tautological notion. But from the sources indicated, it seems to me that the meaning of this sentence is rather that it indicates the impossibility of the hypothetical concept that a definitive specific infinity can be expressed, and in that sense I consider it to be wrong.)

The finiteness of human understanding is very often cited as the reason why only finite numbers can be the subject of thought, but I see in this assertion again the aforementioned circular argument. In the case of the “finiteness of understanding”, it is implicitly meant that mental ability is limited to finite numbers in view of the formation of numbers. If it turns out, however, that the mind is also in a certain sense infinite, in that it can define infinite numbers and distinguish them from one another, then either the words “finiteness of understanding” must be given an expanded meaning, so that that very conclusion can readily be concluded from them, or else the predicate “infinite” must also be used in certain respects for human understanding, which in my opinion is the only correct option. The words “finiteness of understanding”, which one hears so often, do not, I believe, in any way apply; as limited as human nature is, in truth it is much attached to the infinite and I believe that even if it were not itself infinite in many aspects, we all have a firm confidence and certainty regarding the being of the absolute, and in which we all agree is known to be unexplainable. And in particular I take the view that the human mind has an unlimited capacity for the stepwise formation of sets of integers which are related to the infinite steps and whose cardinal-numbers are of increasing magnitude.

The main difficulties in the outwardly different but internally related philosophies of Spinoza and Leibniz can, I believe, be brought closer to the solution by the path I have chosen, and some of them can already be satisfactorily solved and clarified. These are the difficulties which gave rise to the later criticism which, for all its advantages, does not seem to me to provide a sufficient substitute for the inhibited development of the teachings of Spinoza and Leibniz. For alongside or in place of the mechanical explanation of nature, which within its sphere has all the means and advantages of mathematical analysis at its disposal, but whose one-sidedness and inadequacy were so aptly revealed by Kant, there has hitherto not even begun any explanation with the same mathematical rigor that reaches beyond that organic natural explanation. I believe it can only be initiated by resuming and developing the work and efforts of those people.

A particularly difficult point in Spinoza’s system is the relation of the finite steps to the infinite steps; it remains unexplained how and under what circumstances the finite can assert itself against the infinite or the infinite assert its independence against the still stronger infinite. The example already mentioned in § 4 seems to me to indicate in its simple symbolism the way in which one can perhaps come closer to the solution of this question. If ω is the first number of the second number-class, then one has 1 + ω = ω, on the other hand ω + 1 = (ω + 1), where (ω + 1) is a number that is quite different from ω. Everything depends on the position of the finite in relation to the infinite, as we can clearly see here; if the former comes first, it appears in the infinite and disappears into it, but if it is modest and takes its place after the infinite, it is preserved and combines with it to form a new, since modified, infinite.

§ 6 [Properties of infinite integers]

If there are difficulties in conceiving of immeasurably large, self-contained, integers whose magnitudes are comparable to each other, and also to finite numbers, where their relationships to each other and to finite numbers are governed by fixed rules, then these difficulties are connected with a perception that while the new numbers may certainly have the properties of the traditional ones in many respects, in several other respects they have a very strange nature. This perception may be due to the fact that different properties can occur together in a single new number, but which never appear together in a traditional number; they only appear separately in the traditional numbers. In a passage cited in the previous section, one can find the idea that an infinite integer, if it existed, would have to be both even and odd, and since these two properties cannot appear in combination, which leads to a conclusion that such numbers cannot exist.

Apparently there is a tacit assumption that properties which are separate in the traditional numbers must also have this relationship to each other in the new numbers, and from this one concludes that the infinite numbers are impossible. Who doesn’t see the fallacy here? Isn’t every generalization, or extension of terms, associated with giving up specific features, and is even unthinkable without such occurring? Only recently the idea of complex numbers, so important for the development of analysis and leading to the greatest advances, was introduced in spite of the apparent obstacle in the fact that they can be called neither positive nor negative? I am daring only to take a similar step here. Perhaps the common perception will become even more likely to follow me than it was possible to progress from the real numbers to the complex ones; for the new integers, even if they are distinguished by a deeper and more substantial determinateness than the traditional ones, nevertheless, as ordinal-numbers, they have just like the same kind of reality as them, whereas the introduction of the complex numbers was beset by difficulties until they were given a geometrical representation as points or lines in a plane.

In order to come back briefly to that consideration of the even and the odd, let us again consider the number ω, in order to show how those features which are incompatible in finite numbers occur together here without any contradiction. In § 3 the general definitions for addition and multiplication are given, and I have emphasized that in these operations the commutative rule is generally not valid; in this I see an essential difference between infinite and finite numbers. Note that in a product β α the multiplicator is β and the multiplicand is α. It then follows that for ω the following two forms result: ω = ω · 2 and ω = 1 + ω · 2. Accordingly, ω can be understood as both an even and an odd number. But from another point of view, namely, if 2 is taken as the multiplier, it could also be said that ω is neither an even nor an odd number, because, as one can easily prove, it cannot be either in the form of 2 · α nor in the form of 2 · α + 1. The number ω has a very peculiar nature in comparison to the traditional numbers, since all these characteristics and properties are consolidated in it. The other numbers in the second number-class are even more peculiar, as I will later demonstrate.

§ 7 [Diversity of views on the infinite]

Although in § 5 I cited many passages from Leibniz’s works in which he speaks out against infinite numbers by saying, amongst other things:

“Il n’y a point de nombre infini ni de ligne ou autre quantité infini, si on les prend pour des touts veritables.” (There is no infinite number, line or any other infinite quantity, if we take them to be true entire entities).

“L’infini veritable n’est pas une modification, c’est l’absolu; au contraire, des qu’on modifie on se borne ou forme un fini.” (The true infinity is not a modification, it is the absolute; on the contrary, as soon as we modify we limit ourselves or we form a finite).

Here I agree with the first part of the second statement, but not with the second part of it. I am, on the other hand, in the fortunate position of being able to demonstrate statements of the same philosopher in which, to a certain extent, he contradicts himself, when he expresses himself in the most unambiguous way in favor of the truly infinite (as opposed to the absolute infinite). He says in Erdmann p. 118:

“Je suis tellement pour l’infini actuel, qu’au lieu d’admettre que la nature l’abhorre, comme l’on dit vulgairement, je tiens qu’elle l’affecte partout, pour mieux marquer les perfections de son Autour. Ainsi je crois qu’il n’y a aucune partie de la matiere qui ne soit, je ne dis pas divisible, mais actuellement divisée; et par conséquent la moindre particelle doit être considered comme un monde plein d’une infinité de creatures différentes.” (I am so much in favor of the actual-infinite, that instead of admitting that nature abhors it, as one commonly says, I want it to affect it everywhere, so as to better indicate the perfections of its surroundings. So I believe that there is no part of matter that is not actually divided, rather I say that it is divisible; and therefore the smallest particle must be regarded as a world full of an infinity of different creatures).

But Bernhard Bolzano, a highly astute philosopher and mathematician of our century, is the most decisive defender of the actual-infinite, as can be seen, for example, in well-defined point-sets or in the constitution of bodies made of atomic points (I do not mean the chemical-physical, Democritean atoms here because I do not consider that they exist either as a concept, or in reality, regardless of how many useful things are derived to a certain extent by this fiction). Bolzano developed his views in the beautiful and rich script, “Paradoxien des Infendlichen”, Leipzig 1851 (paradoxes of the infinite), the purpose of which is to prove that contradictions in the infinite that over the years have been sought by skeptics and explorers, do not exist at all, provided that one undertakes the difficult task of considering with complete seriousness the true substance of concepts of infinity. In his book one can find a discussion of the mathematical non-actual-infinite that is correct in many respects, such as it occurs in the form of first and higher order differentials or in the summation of infinite series or in other limit processes. This non-actual-infinite (called syncategorematic infinite by some scholastics) is only an auxiliary relational mental concept, which by definition includes variability and for which a “value” can never be assigned in any actual sense.

Bolzano is perhaps the only one with whom the actual-infinite numbers have a certain legitimacy, at least they are often spoken of, but I totally disagree with him in the way he deals with them, since he is not able to establish a correct definition of them. For example, the §§ 29-33 of that book are unfounded and erroneous. The author lacks both the general concept of magnitude and the precise concept of cardinal-number for the real conceptualization of actual-infinite numbers. It is true that both appear in specific forms at individual points, but it seems to me that he does not work it through to full clarity and precision, which explains many inconsistencies and even some errors of this valuable work.

It is most remarkable that there is no essential difference of opinion even among contemporary philosophers with regard to this kind of the infinite, if I may disregard the fact that certain modern schools of so-called positivists or realists (Footnote: Realists: One finds the positivistic and realistic standpoint in relation to the infinite in, for example: Dühring, Natürliche Dialektik, Berlin 1865, p. 109-136 and in von Kirchmann, Katechismus der Philosophie pp. 124-130. See also Ueberweg’s remarks on Berkeley’s Treatise on the principles of human knowledge in von Kirchmann’s Philosophische Bibliothek.
I can only repeat that with regard to the non-actual-infinite I essentially agree with all of these authors; the point of divergence lies only in the fact that they regard this syncategorematic infinite as the only infinite which can be grasped through “expressions” or terms, or even by the mere concept of relationships.
Dühring’s proofs against the actual-infinite could be carried out with much fewer words and seem to me, to either amount to the fact that a definitive finite number, no matter how large one can conceive it to be, can never be infinite, and this follows directly from its concept, or the fact that a variable, infinitely large, finite number cannot be conceived with the property of determinateness, and therefore also cannot have the property of existing, and this in turn results directly from the essence of its variability. For me there is no doubt that this does not make the slightest difference to the conceivability of specific infinite numbers, and yet that argument is held to be evidence against the reality of transfinite numbers. This line of argument seems to me to be similar to when one tries to conclude from the fact that there are innumerable intensities of green that there can be no red. But it is strange that Dühring on p. 126 of his work himself admits, that for the explanation of the “possibility of unlimited creation” there must be a reason which he describes as “understandably completely unknown”. It seems to me that this is a contradiction in terms.
But we also find that thinkers who are close to idealism, or even those who utterly adulate it, deny that there is any justification for actual-infinite numbers.
Chr. Sigwart in his excellent work: Logik, Vol. II. Die Methodenlehre (Tübingen 1878) argues just like Dühring and says on page 47: “an infinite number is a contradictio in adjecto” (contradiction in terms).
Something similar can be found in Kant and J.F. Fries; see the latter’s: System der Metaphysik (Heidelberg 1824) in §51 and §52.
Even the philosophers of the Hegelian school do not accept the actual-infinite numbers; I only mention the meritorious work of K. Fischer, his System der Logik und Metaphysik oder Wissenschaftslehre, 2nd edition (Heidelberg 1865) p. 275. ) or materialists, while they see the greatest concept in this syncategorematic infinite, must concede that it has no actual existence.

But the essentially correct facts can already be found in Leibniz’s work in many places. For example, the following passage relates to this non-actual-infinite (Erdmann, p. 436):

“Ego philosophice loquendo non magis statuo magnitudines infinite parvas quam infinite magnas, seu non magis infinitesimas quam infinituplas. Utrasque enim per modum loquendi compendiosum pro mentis fictionibus habeo, ad calculum aptis, quales etiam sunt radices imaginariae in Algebra. Interim demonstravi, magnum has expressiones usum habere ad compendium cogitandi adeoque ad inventionem; et in errorem ducere non posse, cum pro infinite parvo substituere sufficiat tarn parvum quam quis volet, ut error sit minor dato, unde consequitur errorem dari non posse.” (I hold that philosophically speaking, neither the infinitely small nor the infinitely large are important. For both are mental fictions useful for calculation using approximations, in the same way as imaginary roots in algebra. In the meantime, I have pointed out the usefulness of these expressions as a mental summary as well as for discovery of the infinitely large; they cannot lead into error, as it is sufficient to substitute in it a quantity of sufficient diminutiveness, as for the infinitely small, so that any error should be less than the total, and thus it follows that there can be no resultant error.)

Without the two concepts mentioned, I am convinced that one does not progress any further in the theory of sets, and the same applies, I believe, to those areas which come under the theory of sets or which have the most intimate contact with it, such as, for example, the modern theory of functions on the one hand and from logic and epistemology on the other. To understand the infinite as it occurs to me here and in my earlier attempts gives me real pleasure. I gratefully indulge myself in this pleasure when I see how the concept of integers, which in the finite has only the basic concept of number, but when we rise to the infinite, in some respects the concept splits into two, that of cardinal-number, which is independent of the ordering applied to a set, and that of ordinal-number, for which it is necessary that a regular order is applied to the set (when it becomes a well-ordered set).

§ 8 [The reality of existence of transfinite numbers]

We can speak of the reality or the existence of integers in two ways, the finite and the infinite, but strictly speaking, any concepts or ideas that contemplate their reality apply equally to both. On the one hand, we may regard the integers as real insofar as they occupy a very specific place in our understanding on the basis of definitions, and are well-delineated from all our other mental concepts, and are in certain relationships with them and thus affect our thoughts in a certain way; allow me to call this kind of reality of our numbers their intra-subjective or fundamental reality. (Footnote: What I call the “intrasubjective” or immanent reality of concepts or ideas here should agree with the definition “adequate” in the meaning of this word as used by Spinoza, when he says: Ethica, Part II def. IV, “Per ideam adaequatam intelligo ideam, quae, quatenus in se sine relatione ad objectum consideratur, omnes verae ideae proprietates sive denominationes intrinsecas habet.” (By an adequate idea, I mean an idea which, in so far as it is considered in itself, without relation to an object, has all the properties or intrinsic content of a true idea). ) But reality can also be ascribed to the numbers insofar as they must be taken to be an expression or an image of the processes and relationships of the external world, as opposed to the mind, so that the various number-classes (I), (II), (III) and so on are representatives of cardinal-numbers that actually occur in the physical and the mental realm. I call this second type of reality the trans-subjective or ephemeral reality of the integers.

Given the completely realistic, but at the same time no less idealistic basis of my considerations, there is no doubt for me that these two types of reality always come together in the sense that a term that can be designated as existing in the first respect always has an ephemeral reality in a certain way, and even in infinitely many ways. (Footnote: This conviction essentially agrees with the principles of the Platonist system as well as with an essential feature of the Spinozean system; in the first respect I refer to Zeller, Philosophie der Griechen, 3rd ed. Part 2, 1st section, pp. 541-602. Right at the beginning of the section it says: “Only conceptual knowledge should (according to Plato) grant true knowledge. But as much as our representations are true (Plato shares this presupposition with others, e.g. Pormenides) their objects must also be real, and vice versa. What can be known is; what cannot be known is not, and to the same extent that something is, it is also knowable.
With regard to Spinoza, I need only mention his sentence in Ethica, Part II, Prop. VII: “Ordo et connexio idearum idem est ac ordo et connexio rerum.” (The order and connection of ideas is the same as the order and connection of things).
The same epistemological principle can also be shown in Leibniz’s philosophy. Only since the more recent empiricism, sensualism and skepticism, as well as the resulting Kantian criticalism, does one believe that the source of knowledge and certainty has to be relocated to the senses, or at least to the so-called pure forms of perception of the world of ideas and restricted to them. I am convinced that these elements do not provide any reliable knowledge, because such can only be obtained through concepts and ideas which are at most, only stimulated by external experience, but are mainly formed by internal induction and deduction as something that was, and to a certain extent, is already in us, and only awakened and brought into consciousness. The determination of such, of course, is commonly among the most arduous and difficult tasks of philosophy as it relates to physics, and must often be left to future times, when the natural development of one of the other sciences can reveal the ephemeral meaning of the concept in question.)

This connection between the two realities has as its real reason the unity of the universe which we ourselves belong to. The purpose of my reference to this connection is to derive a conclusion that seems to me very important for mathematics, namely that it only takes into account the fundamental reality of its concepts in the formation of its ideas and is therefore not duty-bound to also examine them according to their ephemeral reality. Because of this exceptional standpoint, which distinguishes it from all other sciences and which provides an explanation for the comparatively easy and unconstrained way of dealing with it, it particularly deserves the name of free mathematics, a designation which I would, if I had the choice, give preference to the term “pure” mathematics that has become common.

Mathematics is completely free in its development and is only bound to the self-evident consideration that its concepts are both free of contradictions and that they are in fixed relationships to proven concepts that have already been previously established. (Footnote: The process in the correct formation of concepts is, in my opinion, the same everywhere; one posits a thing with no uniqueness, which at first is nothing other than a name or a symbol A and gives it properly different, even infinitely many intelligible properties, the meaning of which is known from already existing ideas and which must not contradict one another. This determines the relations of A to the already existing concepts and especially to the related ones. If this is done completely, then all the conditions for awakening the concept A, which slumbered within us, are present and it comes into existence already formed, granted with the intrasubjective reality, which is all that can be demanded of concepts everywhere. It is then a matter of the philosophy of physics to establish its ephemeral meaning. ) In particular, when new numbers are introduced, it is only necessary to give definitions of them which will afford them a sufficient definiteness and, under certain circumstances, such a relationship to the previously established numbers that they can be clearly distinguished from one another in given cases. Once a number satisfies all these conditions, it can and must be considered as existing and real in mathematics. Regarding this one can now see, as indicated in § 4, the reason why one has to consider that the rational, irrational and complex numbers exist, in exactly the same way as we consider the finite positive integers to exist.

It is not necessary, I believe, to fear, as many do, any danger to science in these principles. On the one hand, the specified conditions under which the freedom of number formation can be given are such that they leave an extremely small scope for arbitrariness. In addition every mathematical concept also carries the necessary corrective in itself; if it is sterile or inexpedient, it very soon shows it through its uselessness and it is then dropped because of lack of success. On the other hand, every superfluous constriction of the impulse for mathematical research seems to me to bring with it a much greater danger, and one that is all the greater as no justification can really be drawn for it from the nature of science; for the essence of mathematics lies precisely in its freedom.

Even if this characteristic of mathematics had not been recognized by me for the reasons mentioned, the entire development of science itself, as we perceive it in our century, would still have lead me to exactly the same views.

If Gauss, Cauchy, Abel, Jacobi, Dirichlet, Weierstrass, Hermite, and Riemann always had to subject their new ideas to the control of the philosophy of physics, we would certainly not have been able to enjoy the splendid structure of the modern theory of functions, which, although designed and established completely free of fixed purposes, has, as might be expected, already revealed its ephemeral meaning in applications to mechanics, astronomy and mathematical physics. We would not have seen the great upswing in the theory of differential equations brought about by Fuchs, Poincare, and many others if these magnificent forces had been restrained and constricted by various influences. And if Kummer had not taken the momentous freedom of introducing so-called “ideal” numbers into number theory, we would not be in a position today to admire the important and exceptional algebraic and arithmetical works of Kronecker and Dedekind.

Therefore, although mathematics is entitled to move freely from all fetters of philosophy that relates to physics, on the other hand I cannot grant “applied” mathematics, such as analytical mechanics and mathematical physics, the same right. These disciplines are, in my opinion, pertaining to the philosophy of physics both in their foundations and in their aims; if you seek to free yourself from this, as has recently been suggested by a famous physicist, you select a “description of nature” which must lack the fresh breath of free mathematical thought as well as the power to explain and explore natural phenomena.

§ 9 [Defining the real numbers]

In view of the great importance attached to so-called real, rational and irrational numbers in the theory of sets, I want to state here the most important things regarding their definitions. I will not go into the establishment of the rational numbers, since rigorously arithmetical representations of them have been developed several times. Of those which are best known to me, I highlight those by H. Grassmann (Lehrbuch der Arithmetik, Berlin 1861) and J.H.T. Müller (Lehrbuch der allgemeinen Arithmetik, Halle 1855). On the other hand, I would like to briefly discuss in more detail the three main formats known to me of a rigorously arithmetical definition of real numbers in general, and which are probably all alike in the fundamentals. First there is the format that Prof. Weierstrass has been using for many years in his lectures on analytical functions and of which some hints can be found in the treatise by E. Kossak (Die Elemente der Arithmetik, Berlin 1872). Secondly, Dedekind published a distinctive form of definition in his work Stetigkeit und irrationale Zahlen, Braunschweig, 1872, and thirdly, I gave (Mathematische Annalen, Vol. V, p. 123, 1871) a form of definition that on the surface has a certain resemblance to Weierstrass’s, so much so that they were confused by Weber (Zeitschrift für Mathematik und Physik, Vol. 27, in Historisch literarisch Section, p. 163); in my opinion, however, this third form of definition, also developed later by Lipschitz (Grundlagen der Analysis, Bonn 1877), is the simplest and most natural of all and it has the advantage that it adapts itself most directly to analytical calculus.

These definitions agree that an irrational real number is given by a well-defined infinite set of rational numbers which has the first infinite cardinal-number; they all have this in common. But they differ in the way in which that set is linked to the number it defines, and in the conditions which the set has to fulfill in order to qualify as a foundation for the definition in question.

The first form of definition is based on a set of positive, rational numbers a_v which is denoted by (a_v). The numbers satisfy the condition that regardless of how many of a finite number of them are summated, their sum is a finite quantity that always remains below a specified limit. If one has two such sets (a_v) and (a_v′ ), it may be rigorously shown that they can present as one of three cases:

1. when a finite number of elements are collected from each set, and where there is no limit to such finite number of elements, each part ¹⁄_n of unity is always contained in both such collections, or
2. for all parts ¹⁄_n from a certain n on, the first set will contain more parts than the second, or
3. for all parts ¹⁄_n from a certain n on, the second set will contain more parts than the first

Corresponding to these occurrences, if b and b′ are the numbers defined by the two sets (a_v) and (a_v′ ), in the first case b = b′, in the second b > b′, in the third b < b′. If the two sets are combined into a new one (a_v + a_v′ ), this gives the basis for the definition of b + b′. But if one forms from the two sets (a_v) and (a_v′ ) the new (a_v · a_μ′ ), in which the elements are the products of all a_v and all a_μ′, this new set is taken as the basis of the definition for the product bb′.

One sees that here the generation, which links the set with the number to be defined by it, lies in the formation of the sum. However, it must be emphasized as essential that only the summation of an always finite number of rational elements is used and that the number b is not defined at the outset as the sum ∑a_v of the infinite series (a_v). That would be a logical error here, because the definition of the sum ∑a_v can only be obtained by equating it with the completed number b, which must have already been defined. I believe that this logical mistake, which was avoided only by Weierstrass, was almost universally committed in earlier times and was not noticed because it is one of the rare cases in which real mistakes cannot cause any significant damage in the calculation. Nevertheless, according to my conviction, all the difficulties which have been found in the concept of the irrational are connected with the above-mentioned error, whereas if this error is avoided the irrational numbers are fixed in our minds with the same definiteness, distinctness and clarity as the rational numbers.

Dedekind’s form of definition is based on the set of all rational numbers, but divided into two groups in such a way that if the numbers in the first group are denoted by U_v, and those of the second group are denoted by B_v where U_v < B_v always applies; Dedekind calls such a division of the rational set of numbers a “cut” and denotes it by (U_v | B_v) and assigns a number b to it. If one compares two such cuts (U_v | B_v) and (U_v′ | B_v′ ) with one another, then, as in the case of the first definition, there are three possibilities, corresponding to the numbers b and b′ represented by the two cuts are equal to each other or else b > b′ or b < b′. The first case occurs (apart from certain exceptions which occur when the numbers to be defined are rational, and are easy to rule for) only if the two cuts are completely identical and here comes the decisive advantage of this form of definition over the other two, which cannot be denied, that each number b corresponds to only one cut, which is countered by the great disadvantage that the numbers in analysis are never in the form of cuts, a form which they must first be brought into with great effort and laboriousness.

Now here also the definitions for the sum b + b′ and the product b b′ follow from the two given previous cuts to give the basis of new definitions.

The disadvantage associated with the first and second form of definition, is that the same (i.e: identical) numbers are presented infinitely often and thus a clear overview of all real numbers is not immediately obtained. This disadvantage can be eliminated with the greatest ease by ensuring that the sets (a_v) used are completely specified and fully determined sets, by using any of the known unambiguous system types, such as the decimal system or by simple continued fraction expansions.

I now come to the third form of definition of real numbers. Here too, an infinite set of rational numbers (a_v) is taken with the property of the first infinite cardinal-number, but a different property is required of it compared to the Weierstrassian form of definition. This requires that, after assuming an arbitrarily small rational number ε, a finite number of terms of the set can be separated so that the absolute value of the difference between any remaining pairs of terms is always smaller than ε. Any such amount (a_v), which can also be characterized by the requirement:

I call a fundamental sequence and assign to it a number b that may be defined by it, and it is also appropriate to use the sign (a_v) to designate it, as done by Heine, who proposed such to me after many oral discussions with me on these matters. (See Crelle’s Journal, Vol. 74 p. 172). Such a fundamental sequence presents three cases that can be rigorously deduced from its definition, either:

1. their terms a_v for sufficiently large values ​​of v are smaller in absolute value than any arbitrarily given number, or
2. from a certain v onwards they are greater than a determinate specific positive rational number ρ, or
3. from a certain v onwards they are smaller than a determinate specific negative rational quantity - ρ.

In the first case I say that b is equal to zero, in the second that b is greater than zero or positive, and in the third case that b is less than zero or negative.

Now come the elementary operations. If (a_v) and (a_v′ ) are two fundamental sequences by which the numbers b and b′ are determined, then it turns out that (a_v ± a_v′ ) and (a_v · a_v′ ) are also fundamental sequences, which gives three new terms which serve as definitions for the sum and difference b ± b′ and for the product b · b′.

Also, if b is not zero, for which the definition is given above, one proves that (^a_v′⁄_av ) is also a fundamental sequence, the associated number of which provides the definition for the quotient ^b′⁄_b.

The elementary operations between a number b given by a fundamental sequence and a directly given rational number a are included in the terms just established by letting a_v′ = a and b′ = a.

Only now do we have the definitions of equal, greater and smaller for two numbers b and b′ (of which b′ can also be = a), namely that b = b′ or b > b′ or b < b′ applies depending on whether b - b′ is equal to zero, or greater than zero, or less than zero.

After all these preparations, the first rigorously provable theorem is that if b is the number determined by a fundamental sequence (a_v), as v increases b - a_v becomes smaller in absolute terms than any conceivable rational number, or:

Attention should be paid to this essential point, the meaning of which can easily be overlooked: in the third form of definition, the number b is not defined as the limit of the terms a_v of a fundamental sequence (a_v). This would be a logical error similar to that emphasized in the discussion of the first form of definition, namely for the reason that the existence of the limit Lim_{v = ∞} a_v would be assumed. On the contrary, the situation is the other way round, so that by our previous definitions the term b has been given such properties and relationships to the rational numbers that the conclusion can logically be drawn from this: Lim_{v = ∞} a_v exists and is equal to b. Forgive me for the detail here, for which I am motivated by the perception that most people pass by this inconspicuous trifle and are then are easily entangled in doubts and contradictions with regard to the irrational, from which they would be completely spared if the reasoning emphasized here was observed. They would then clearly recognize that the irrational numbers, by virtue of the properties given to them by the definitions, have a reality in our minds that is just as certain as for the rational numbers, and just like for the integers, and that it does not have to be obtained by a limiting process but rather, on the contrary, one can in general be convinced, by such possession of that reality in our minds, of the efficiency and soundness of the limiting processes. (Footnote: Translator’s note: Cantor’s has two footnote references that point to the same footnote; here for convenience we simply repeat it:
The process in the correct formation of concepts is, in my opinion, the same everywhere; one posits a thing with no uniqueness, which at first is nothing other than a name or a symbol A and gives it properly different, even infinitely many intelligible properties, the meaning of which is known from already existing ideas and which must not contradict one another. This determines the relations of A to the already existing concepts and especially to the related ones. If this is done completely, then all the conditions for awakening the concept A, which slumbered within us, are present and it comes into existence already formed, granted with the intrasubjective reality, which is all that can be demanded of concepts everywhere. It is then a matter of the philosophy of physics to establish its ephemeral meaning.) And now it is easy to expand the theorem just cited to the following: If (b_v) is any set of rational or irrational numbers with the condition that

then there is a number b determined by a fundamental sequence (a_v) such that:

I call such a fundamental sequence (a_v) a fundamental sequence of the first order. It turns out that these same numbers b which are defined on the basis of these fundamental sequences of the first order (a_v), in such a way that they identify themselves as limits of a_v , can also be represented in several ways as limits of sequences (b_v), where each b_v is defined by a fundamental sequence of the first order (a_μ^(v) ) (with a fixed v ).

I therefore call such a set (b_v), a fundamental sequence of the second order if it satisfies the condition that

Fundamental sequences of the third, fourth, …, n^th order, can also be formed, but also fundamental sequences of the α^th order, where α is any number of the second number-class. All these fundamental sequences do exactly the same thing for the determination of a real number b as the fundamental sequence of the first order, and the difference lies only in the more complex, more extensive form that is given. Nevertheless, if one wishes to take the standpoint of the third form of definition, it seems to me to be highly appropriate to set out this difference in the manner indicated, as I have done in a similar way in Mathematische Annalen, Vol. 5, p. 123, 1872). I therefore now use the expression:

The quantity b is given by a fundamental sequence of the n^th or α^th order.

If one decides to do this, one achieves an extraordinarily flexible and at the same time comprehensible language in order to describe the richness of the various, often complex system of analysis in the simplest and most characteristic way, which in my opinion is a gain in clarity and certainty that should not be underestimated. I hereby counter the misgivings that Dedekind expressed in the preface to his work “Stetigkeit und irrationale Zahlen” with regard to these distinctions; while my intention was inclined towards introducing new numbers through the fundamental sequences of the second, third order, etc., which could not already be determined by the fundamental sequences of the first order, I had in mind only the concept of such different forms; this is evident from individual passages in my work.

I would like to draw your attention to a remarkable circumstance, namely that in these orders of fundamental sequences, which I distinguish by numbers of the first and second number-class, all conceivable forms in analysis with the usual sequential character (those already discovered and those not yet discovered) are completely included in the sense that there is no fundamental sequence whose ordinal-number can be determined by a number of, for example, the third number-class, as I shall rigorously prove on another occasion.

I shall now try to briefly assess the usefulness of the third form of definition.

To denote that a number b is given on the basis of a fundamental sequences (e_v ) of any order n or α, I use the formulas:

b ~ (e_v )  or  (e_v ) ~ b

For example, if there is a convergent series with the general term c_v , the necessary and sufficient condition for convergence is, as is well known, that:

The sum of the series is therefore defined by the formula:

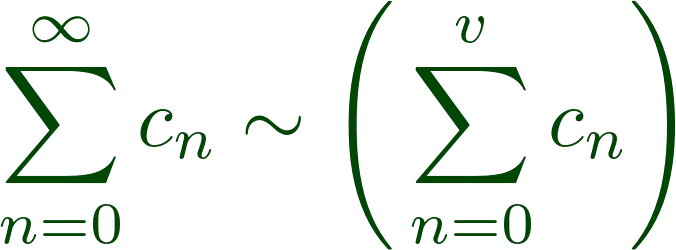
If, for example, all c_n are defined on the basis of a fundamental sequence of the k ^th order, then the same apples for

where the sum

is here defined by a fundamental sequence of (k + 1)^th order.

If, for example, the conceptual content of the sentence sin (^π⁄₂) = 1 is to be defined, one can think of (^π⁄₂) and its powers as given by the formulas:

^π⁄₂  ~  (a_v) ,   (^π⁄₂)^2m + 1  ~  (a_v^2m + 1)

which we can abbreviate as:

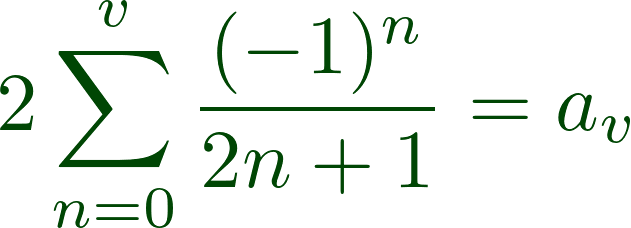
In addition, we also have:

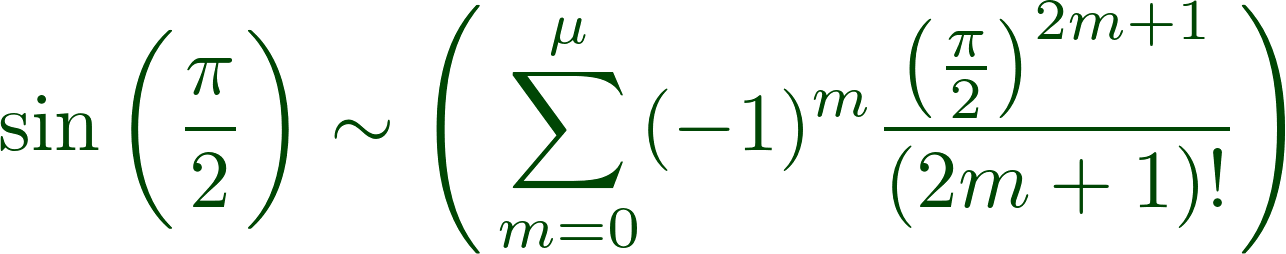
so that sin (^π⁄₂) is defined on the basis of a fundamental sequence of the second order, and this proposition expresses the equality of the rational number 1 and the number sin (^π⁄₂) as derived on the basis of a fundamental sequence of the second order.

In a similar way, the conceptual content of more complex formulas, such as those from the theory of theta functions, can be described precisely and relatively simply - while the conversion of infinite sequences in general to sequences made up purely of rational elements, especially when such are required to be all of the same sign and to converge unconditionally, is usually associated with the greatest inconvenience.

This is completely avoided here by the third form of definition, in contrast to the first, and which can obviously also be avoided, provided one is not finding a numerical approximation of the sum of a series whose terms are rational numbers, but only when it is absolutely necessary to have precise definitions. The first form of definition does not seem to me to be so easy to use when it comes to the precise definition of the summations of series which do not necessarily converge, but in which the arrangement of their positive as well as negative terms is definitely predetermined. But even in the case of series with unconditional convergence, the generation of the sum, even if it is independent of the ordering, can only really be carried out with some specific ordering; in such cases, therefore, one is tempted to give preference to the third form of definition over the first. Finally, it seems to me that the third form of definition is supported by its ability to generalize to transfinite numbers, while such a development is quite impossible for the first form of definition This difference is simply due to the fact that in the case of infinite numbers the commutative rule is in general invalid for addition, while the first form of definition is inextricably linked with this rule, and it stands and falls with it. But for all types of numbers where the commutative rule of addition is valid, the first form of definition proves to be quite excellent, apart from the points already mentioned.

§ 10 [The continuum]

The concept of the “continuum” has not only played an important role everywhere in the development of the sciences, but has also always caused the greatest differences of opinion and even angry disputes. Perhaps this is due to the fact that its conceptual basis appears quite different to the dissenters, and the reason for this is that the precise and complete definition of the concept has not been communicated to them. It is perhaps also the case, which seems most probable to me, that the concept of the continuum originated with the Greeks, but without the necessary clarity and completeness that would obviate the possibility that subsequent thinkers would perceive it in diverse ways. Thus we see that Leucippus, Democritus and Aristotle regard the continuum as a composite, which consists of endlessly divisible particles (ex partibus sine fine divisibilibus), whereas Epicurus and Lucretius consider that it is a composite of atoms that are finite things. From this a great dispute later arose among philosophers, some of whom followed Aristotle, while others followed Epicurus, while others, in an attempt to steer clear of the dispute, sided with Thomas Aquinas (Footnote: Thomas Aquinas, Opuscula, XLII De natura generis, Ch.19 et 20; LII De natura loci; XXXII De natura materiae et de dimensionibus interminatis. See: C. Jourdin, La Philosophie de Saint Thomas d’Aquin, pp. 303-329; K. Werner, Der Heilige Thomas von Aquino (Regensburg 1869), Vol. 2 pp. 177-201. ) in the claim that the continuum consists neither of an infinite number nor of a finite number of parts, but of no parts at all. This opinion seems to me more of a tacit admission that one has not got to the root of the matter, preferring to avoid it in a polite manner, rather than being any explanation of the facts. Here we observe the medieval-scholastic origin of a view that we still find to be held today, according to which the continuum is an indivisible concept or, as others put it, a notion that is purely a priori, and hardly amenable as a basis for any definition. Every attempt at an arithmetical determination of this mystery is regarded as an inadmissible interference and rejected with all due intensity, and those of a diffident disposition get the impression that the “continuum” is not a mathematical-logical notion but rather a religious dogma.

Far be it from me to conjure up these issues again, nor would I have the space to discuss them more precisely within this restricted framework. I only see myself obliged to develop here, as briefly as possible, the concept of the continuum as logically and soberly as I understand it and only as it is required for the mathematical theory of sets. This process has not been easy for me because, of all the mathematicians whose authority I would like to appeal to, not a single one of them has dealt with the matter more closely than I in the sense that is required here.

On the basis of one or more real or complex continuous quantities (or, I believe, more correctly expressed as sets of continuous quantities) one has the concept of a continuum which is dependent on a single or many such sets. The concept of a continuous function has developed in the best possible way in the most diverse of directions, and in this way the theory of so-called analytical functions has arisen, as well as of more general functions with very remarkable properties (such as non-differentiability and the like). But the continuum itself as an independent entity has only been assumed by mathematical authors in its simplest form and has not been subjected to any more detailed consideration.

But first, I have to explain that in my opinion, the use of the concept of time or the intuition of time is not applicable when discussing the much more fundamental and general concept of the continuum. In my opinion, time is a notion which requires for any clear explanation of it, a presupposition of the concept of continuity, a concept that is independent of it. Even with the aid of the concept of continuity, time cannot be conceived either objectively as a substance or subjectively as a necessary a priori form of perception. Time is nothing more than an auxiliary and relational concept through which, by way of our perceptions, we establish the relationship between different motions occurring in nature. A thing such as objective or absolute time does not occur anywhere in nature and therefore time cannot be used as a measure of movement. Such motion might be regarded as a measure of time, were it not for the fact that time, even in the modest role of a subjectively necessary a priori form of perception, has not been able to bring about any useful, incontrovertible benefit, even though since Kant there has been plenty of time for this to happen.

It is also my conviction that one cannot do anything with the so-called intuition of space in order to gain information about the continuum, since space and the structures imagined in it can only achieve such information along with the help of the concept of an already completed continuum - in which case they are not the subject of mere aesthetic considerations, philosophical insight, or imprecise comparisons, but more sober and exact mathematical investigations.

Hence I have no choice but to attempt, with the help of the real number concepts defined in § 9, to form a purely arithmetical concept of a point continuum that is as general as possible. The basis for this, as it cannot be otherwise, is the n-dimensional plane arithmetical space G_n, i.e: the set of all value systems:

(x₁ | x₂ | … | x_n )

in which each x can receive all real numerical values from - ∞ to + ∞ independently of the others. Every specific value system of this kind is called an arithmetical point of G_n. The distance between two such points is given by the expression:

| √(x₁ - x₁)² + (x₂ - x₂)² + … + (x₁ - x₁)² |

An arithmetical point-set P contained in G_n is to be understood as any rule-based definition of a point-set of the space G_n. The analysis therefore comes down to establishing a precise definition for when P is to be called a continuum, but which is at the same time as general as possible.

I have proved (Crelle’s Journal, Vol. 84, p. 242) that all spaces G_n, no matter how large the so-called dimensional number n, have the same cardinal-number and consequently have the same cardinal-number as the linear continuum, such as the set of all real numbers in the Interval (0,1). The analysis and determination of the cardinal-number of G_n is therefore reduced to the same question, specialized to the interval (0,1), and I hope to be able to answer this soon by a rigorous proof that the cardinal-number sought is none other than that of our second number-class (II). (Footnote: Translator’s note: Here Cantor states what is now known as the Continuum Hypothesis, and his expectation that he will be able to prove it. ) From this it follows that all infinite point-sets P have either the cardinal-number of the first number-class (I) or the cardinal-number of the second number-class (II). Another conclusion can be drawn from the fact that the set of all functions of one or more variables which can be represented by a given infinite series (regardless of the actual series), also only has the cardinal-number of the second number-class (II) and therefore is countable by numbers of the third number-class (III). (Footnote: Even the set of all continuous, but also the set of all integratable functions of one or more variables, should only have the cardinal-number of the second number-class (II). However, if one drops all restrictions and considers the set of all continuous and discontinuous functions of one or more variables, then this set has the cardinal-number of the third number-class (III). ) This proposition will refer, for example, to the set of all “analytical” functions, i.e: functions of one or more variables that result from the continuation of convergent power series, or to the set of all functions of one or more real variables that can be represented by trigonometric series.

In order to come closer to the general concept of a continuum located within G_n, I refer to the concept of the derivative P ⁽¹⁾ of an arbitrarily given point-set P, as I first used it in the work: Mathematische Annalen Vol. V, then developed in Vol. 15, 17, 20 and 21 and expanded to the concept of a derivative P ^(γ), where γ is any integer from one of the number-classes (I), (II), (III) etc. (Footnote: Translator’s note: These following paragraphs (9-11 of §10 in the original) were later withdrawn as erroneous by Cantor in §16 of the sixth part of this work, Mathematische Annalen, 23, 453-488 (1884); Hallett provides a discussion in Cantorian set theory and limitation of size. Clarendon Press, Oxford, 1984, p. 91-93.)

Although these two predicates “reducible” and “perfect” are incompatible in the same point-set, on the other hand as one can easily see with a little attention, irreducible is not the same as perfect, and similarly imperfect is not exactly the same as reducible.

The interior of the perfect point-set S is definitely not always what I have called “everywhere-dense” in my work mentioned above; (Footnote: The theorem can be proved that perfect sets never have the cardinal-number of (I). I give as an example of a perfect point-set, which is not everywhere-dense in any interval, however small, the set of all real numbers given by the formula:
z = ^c₁ ⁄₃ + ^c₂ ⁄_3² + … + ^c_v ⁄_3^v + …
where the coefficients c_v arbitrarily take the two values 0 and 2, and the series can consist of a finite number or an infinite number of elements. ) therefore, they are not suitable on their own for the complete definition of a point continuum, even if one must immediately concede that a point continuum must always be a perfect set.

Instead, one more concept is required in order to define the continuum along with the preceding one, namely the concept of a connected point-set T .

We call T a connected point-set if for every two points t and t′ of it, given an arbitrarily small number ε, there is always in multiple ways a finite number of points t₁, t₂, … t_v of T where the distances tt₁, t₁t₂, t₂t₃, … t_vt′ are all smaller than ε.

It is now easy to see that all geometrical point continuums known to us also fall under this concept of a connected point-set; but I now believe that I have determined that the necessary and sufficient features of a point continuum are given by these two predicates “perfect” and “connected” and therefore I define a point continuum within G_n as a perfectly-connected set. (Footnote: Note that this definition of a continuum is free from any reference to what is called the dimension of a continuous structure. The definition also includes such continuums, which consist of connected sections of various dimensions, such as lines, surfaces, solids, etc. On a later occasion I will show how one can progress from this general continuum to more specific continuums with a certain dimension. I know very well that the word “continuum” has not yet taken on a fixed meaning in mathematics, and although my definition of it is a balanced mean, it will therefore be judged by some to be too narrow and by others to be too broad.
In my opinion, a continuum can be understood as a perfect and connected structure. According to this, for example, a straight line which lacks one or both endpoints, and a circular area from which the boundary is excluded, are not complete continuums; I call such point-sets semi-continuums.
In general, I understand by a semi-continuum an imperfect, connected point-set belonging to the second number-class, which is so constituted that any two points of it can be connected by a complete continuum, which is a component of this point-set. For an example, the set that I call 𝔘 in Mathematische Annalen. Vol. 20, p. 119, arises from G_n by removing any point-set of the first cardinal-number, and is a semi-continuum.
The derivative of a connected point-set is always a continuum, hence it is irrelevant whether the connected point-set has the first or the second cardinal-number.
If a connected point-set is of the first cardinal-number, I cannot call it either a continuum or a semi-continuum.
With the concepts that I have placed at the forefront of the theory of sets, I make it my mission to investigate the common structures of algebraic as well as transcendental geometry according to all their possibilities, whereby the generality and sharpness of the results will hardly be surpassed by any other method.) Here “perfect” and “connected” are not mere words, but quite general predicates of the continuum which are conceptually characterized in the most precise possible way by the preceding definitions.

Bolzano’s definition of the continuum (Paradoxien § 38) (Footnote: B. Bolzano, Paradoxien des Unendlichen, CH Reclam, 1831. ) is certainly incorrect; it only expresses one single property of the continuum, which is also satisfied in sets which result from G_n by “isolating” some point-set at a distance from G_n (cf. Mathematische Annalen Vol. 21, p. 51); it is likewise satisfied by sets which consist of several separate continuums. It is evident that there is no continuum in such cases, although according to Bolzano this would be the case. So here we see a violation of the sentence: “ad essentiam alicujus rei pertinet id, quo dato res necessario ponitur et quo sublato res necessario tollitur; vel id, sine quo res, et vice versa quod sine re nec esse nec concipi potest.” (It is the essence of any entity that, if something is judged necessary to it, then if that thing is taken away, the entity is lacking that thing; or for any other similar thing, without which the entity can neither be nor be conceived, but with them it can be.)

Similarly, it seems to me that Dedekind rather one-sidedly emphasizes only another property of the continuum in his article (Stetigkeit und irrationale Zahlen), namely the property that it has in common with all “perfect” sets.

§ 11 [Ordinal-numbers]

It will now be shown how we progress to the definition of the new numbers, and how the natural segmentation into what I call number-classes results from the absolutely infinite sequence of actual integers. To this discussion I will only add the main propositions about the second number-class and its relation to the first. The sequence (I) of positive actual integers 1, 2, 3, …, v, … has its origin in the repeated positioning and combination of elemental units that are regarded as all identical; the number v is the expression both for a definite finite number of such successive positions, as well as for the union of the positioned units into a whole. The formation of finite integers is based on the principle of adding a unit to an existing number that has already been formed; I call this principle, which, as we shall soon see, also plays an essential role in the generation of the higher integers, the first principle of generation. The cardinal-number of the numbers v of the number-class (I) which is formed in this way is infinite; there is no largest one of these numbers v. ​As contradictory as it would be to speak of a largest number in the number-class (I), on the other hand it is not abhorrent to think of a new number, which we want to define as ω, (Footnote: The sign ∞, which I used in Part 2 of this work (Mathematische Annalen Vol. 17, p. 357), I replace from now on with ω, because the sign ∞ is already often used to denote non-actual infinities. ) and which is to be an expression for the fact that the natural succession of the complete number-class (I) is given according to established rules (similarly, v is an expression for the fact that a certain finite number of units are combined into a whole). It is even permissible to think of the newly created number ω as the limit towards which the numbers v approach, provided nothing else is understood by that, so that ω is to be the first integer that follows all numbers v, i.e: is to be called larger than each of the numbers v. By allowing further positions of the unit to follow the positioning of the number ω, further numbers are obtained with the aid of the first principle of generation:

ω + 1, ω + 2, …, ω + v, …

Since again one does not arrive at a largest number here, one conceives of a new one, which one calls 2ω and which should be the first one that follows all previous numbers v and ω + v. If one applies the first principle of generation repeatedly to the number 2ω, one arrives at the continuation:

2ω + 1, 2ω + 2, …, 2ω + v, …

of the previous numbers.

This logical operation, which has given us the two numbers ω and 2ω, is obviously different from the first principle of generation; I shall call this the second principle of generation of integers and I define it more precisely thus: If there is any definite succession of defined integers of which there is no largest integer, a new number is created on the basis of this second principle of generation, which is thought of as the limit of those numbers, i.e: defined as the next number larger than all of them.

Through the combined application of both principles of generation one thus successively obtains the following continuations of our numbers obtained so far:

3ω + 1, 3ω + 2, …, 3ω + v, …

…,   …,   …,   …

μω + 1, μω + 2, …, μω + v, …

…,   …,   …,   …

However, this does not lead to an endpoint either, because none of the numbers μw + v is a largest number.

The second generation principle therefore prompts us to introduce the next number that follows all numbers μw + v, which can be called ω², and which is followed by the definite succession numbers:

λω + μω + v

and following the two principles of generation it is then apparent that we arrive at numbers of the following form:

v₀ω^μ + v₀ω^μ-1 + … + v_μ-1ω + v_μ

but then the second principle of generation drives us to define a new number, which is to be the next largest of these numbers and which is referred to by:

ω^ω

As one can see, there is no end to the formation of new numbers. If both principles of generation are followed, one always obtains new numbers and sequences of numbers that have a completely determined succession.

One is thereby initially given the impression that this way of forming new whole definitive-infinite numbers would cause us to lose ourselves in limitlessness, and that we would be unable to give this endless process a certain temporary termination, in order to thereby impose a similar restriction point, as it actually exists in a certain sense in relation to the first number-class (I); only the first principle of generation was used there, making it impossible to step out of that sequence (I). The second principle of generation is required to not only lead beyond the previous numerical domain, but also proves to be a means by which, in conjunction with the first principle of generation, we are enabled to break through every barrier in the formation of the concept of integers.

But if we now note that all the numbers obtained so far, and those immediately following them, satisfy a certain property, then this property provides us with a new third principle in addition to these two, if we impose it as a condition on the formation of all new numbers. (Footnote: Translator’s note: Rather than providing a definition of this third principle here, he gives an instance in the following paragraphs. ) I call this the principle of limitation or restriction which, as I will show, has the effect that the second number-class (II), defined by the inclusion of this third principle, not only obtains a greater cardinal-number than that of the first number-class (I), but precisely the next higher cardinal-number, the second cardinal-number.

One is at once convinced that the property mentioned, which is satisfied by each of the infinite numbers α previously defined - that the set of the numbers preceding this number in the sequence of numbers has the cardinal-number of the first number-class (I). Take for example, the number ω^ω; the preceding ones are included in the formula:

v₀ω^μ + v₀ω^μ-1 + … + v_μ-1ω + v_μ

where μ, v₀, v₁, …, v_μ are all finite positive integers, including zero but excluding the case where v₀ = v₁ = … = v_μ = 0.

As is well known, this set can be brought into the form of a simple infinite sequence and thus has the cardinal-number of the first number-class (I).

Furthermore, for every sequence of sets, where each set is of the first infinite cardinal-number, then provided that sequence itself is of the first infinite cardinal-number, it always results in a set which has the cardinal-number of the first number-class (I), and it is clear that if we continue our sequence of numbers we only ever obtain numbers which actually satisfy that condition.

We therefore define the second number-class (II) as the set of all numbers α that can be formed with the aid of the two principles of generation and which progress in a definitive succession:

ω, ω + 1, …, v₀ω + v₀ω^μ-1 + … + v_μ-1ω + v_μ, …, ω^ω, …, α, …

which are subject to the condition that all of the numbers preceding α, from 1 on, form a set with the cardinal-number of the first number-class (I).

§ 12 [Cardinal-numbers]

The first thing we now have to show is the theorem that the new number-class (II) has a cardinal-number that is different from that of the first number-class (I).

This proposition results from the following proposition:

The proof of this proposition is simply as follows: In the sequence (α_v) let α_x2 be the first number which is greater than α₁, and α_x3 the first number which is greater than α_x2 and so on.

One then has:

1 < x₂ < x₃ < x₄ < …

α₁ < α_x2 < α_x3 < α_x4 < …

and

α_v < α_xλ

whenever

v < x_λ

Here it can occur that from a certain number α_xρ on, all numbers in the sequence (α_v) that follow it are smaller than it; then it is obviously the largest of them all and we have: γ = α_xρ . Otherwise, consider the set of all integers from 1 onwards that are smaller than α₁, and first add to this set, the set of all integers which are ≥ α₁ and < α_x2, then the set of all numbers which are ≥ α_x2 and < α_x3 and so on, one then obtains a definitive subset of consecutive numbers of our first two number-classes. This set of numbers most obviously is of the first infinite cardinal-number, and therefore there exists (according to the definition of the second number-class (II)) a certain number β of the number-class (II), which is the next largest to those numbers, and so we have β > α_xλ and therefore also β > α_v because x_λ can always be assumed to be so large that it becomes larger than a given v and because then α_v < α_xλ .

On the other hand, it is easy to see that every number β ′ < β is surpassed in size by certain numbers α_xv , by which all parts of the theorem are now proved.

From this follows the proposition that the set of all numbers of the second number-class (II) does not have the cardinal-number of the first number-class (I); because otherwise we would get the integer number-class (II) in the form of a simple sequence:

α₁, α₂, …, α_v …

and so it must have, according to the proposition just proved, either a largest term γ or all its terms α_v would be exceeded by a specific number β from (II). In the first case the number γ + 1 belongs to the second number-class (II), while in the second case the number β would belong to the second number-class (II) and could not appear in the sequence (α_v), otherwise, by the already assumed properties of the sets (II) and (α_v), there would be a contradiction. Therefore the second number-class (II) has a different cardinal-number than the first number-class (I).

For the two cardinal-numbers of the number-classes (I) and (II) it is really the case that the second is the cardinal-number that follows the first infinite cardinal-number, that is, there are no other cardinal-numbers between these two cardinal-numbers, and this fact emerges with absolute certainty from a proposition which I will shortly state and prove.

However, if we first take a look backwards at the means that have led both to an expansion of the concept of integers and to a new collection of different but well-defined sets, we observe that there were three prominent, but quite distinct logical principles. There are both the two principles of generation defined above and then also the additional principle of limitation or restriction, which consists of the requirement that the creation of a new integer using one of the other two principles is permitted only if the set of all preceding numbers has the cardinal-number of an already existing, defined number-class. In this way, by observing these three principles, one can arrive at ever new sets of numbers with the greatest logical certainty, and with them all the different, successively ascending cardinal-numbers that occur in the physical and conceptual realms, and the new numbers obtained also have the same concrete determinateness and objective reality as the earlier ones; I therefore really do not know what should hold us back from this activity of forming new numbers, once it appears that the introduction of a new one of these innumerable number-classes has become desirable or even indispensable for the advancement of science.

§ 13 [Succession of cardinal-numbers]

I now come to the promised proof that the cardinal-numbers of (I) and (II) follow upon one another directly, so that there are no other cardinal-numbers in between. If one chooses a set (α′ ) of different numbers α′ from the number-class (II) according to some rule, i. e., any set (α′ ) contained within (II), then such a set always has peculiarities, which can be expressed in the following sentences:

“There is always a smallest number in the numbers of the set (α′ ).”

and

“If, specifically, one has a sequence of numbers of the number-class (II): α₁, α₂, …, α_β … which continuously decrease in size (so that α_β > α_β′ if β > β′ ), then this sequence necessarily terminates with a finite number of elements and ends with the smallest of the numbers; the sequence cannot be infinite.”

It is remarkable that this proposition, which is immediately clear when the numbers are finite integers α_β can also be demonstrated in the case of infinite numbers α_β . Indeed, according to the previous proposition, which can easily be seen from the definition of the sequence of numbers (II), there is a smallest number among the numbers α_v if one only considers those ones for which the index v is finite; if for some ρ this number is = α_ρ, then it is evident that α_v > α_v + 1 and the sequence α_v and thus also the entire sequence α_β must consist exactly of ρ elements, and so it is a finite sequence.

Now one obtains the following fundamental proposition: “If (α′) is any set of numbers contained in the number-class (II), only the following three cases can occur:

1. (α′ ) is a finite set, i.e: it consists of a finite number of numbers, or
2. (α′ ) has the infinite cardinal-number of the first class, or
3. (α′ ) has the infinite cardinal-number of (II).”

Quartum non datur (The fourth is not given).

The proof can be carried out as follows: let Ω be the first number of the third number-class (III); then, because the latter is contained in (II), all the numbers α′ of the set (α′ ) are smaller than Ω.

We now think of the numbers α′ in order of their size; α_ω is the smallest among them, α_ω + 1 the next largest, etc., so that the set (α′ ) is obtained in the form of a “well-ordered” set α_β, where β runs through numbers of our natural extended number sequence from ω on. Obviously β always remains less than or equal to α_β and since α_β < ω, then β < ω. The number β cannot therefore go beyond the number-class (II), but remains within its domain; therefore only three cases can take place:

1. β remains below a specific number in the sequence w + v, in which case (α′ ) is a finite set, or
2. β assumes all values ​​of the sequence w + v, but remains below a specific number of sequence (II), in which case (α′ ) is obviously a set of the first cardinal-number, or
3. β assumes arbitrarily large values ​​in (II), in which case β runs through all the numbers in (II); in this case the set (α_β), i.e: the set (α′ ) has evidently the cardinal-number of (II).

so the proposition is proved.

As a direct result of the theorem just proved, the following apply:

“If one has some well-defined set M of the cardinal-number of the number-class (II) and takes some infinite subset M′ of M, the set M′ can either be thought of in the form of a simply infinite sequence, or it is possible to map both sets M′ and M to correspond one-to-one to each other.”

“If one has any well-defined set M of the cardinal-number of the number-class (II), a subset M′ of M and a subset M′′ of M′ and if one knows that M′′ can be mapped one-to-one to M, then M′ can be mapped one-to-one to M, and also to M′′ .”

I make this last assertion here because of the connection with the preceding ones, given the condition that M has the cardinal-number of (II); it is also obviously correct if M has the cardinal-number of (I). This appears to me to be most remarkable, and I therefore emphasize this expressly, that this proposition has general validity, regardless of the cardinal-number of the set M. I will go into this in more detail in a later article and then demonstrate the peculiar interest which is attached to this general proposition.

§ 14 [Operations on transfinite numbers]

In conclusion, I will now consider the numbers of the second number-class (II) and the operations that can be carried out with them, but on this occasion I will limit myself to what is most obvious, and reserve the publication of detailed investigations on them for later.

I defined the operations of adding and multiplying in general terms in § 3 and showed that for infinite integers they are generally not subject to the commutative rule, but are subject to the associative rule; this also applies in particular to the numbers in the second number-class. With regard to the distributive rule, it is only generally valid in the following form:

(α + β ) y = αy + βy

where α + β, α, and β appear as multipliers, as can be seen directly from inner intuition.

Subtraction can be viewed in two ways. If α and β are any two integers, α < β, it is easy to convince oneself that the equation:

α + ξ = β

always allows one and only one solution for ξ, where, if α and β are numbers from (II), then ξ will be a number from (I) or (II). This number ξ is set equal to β - α. On the other hand, consider the following equation:

ξ + α = β

where it often turns out that it is not solvable for ξ. For example such a case occurs in the following equation:

ξ + w = w + l .

But in those cases where the equation ξ + α = β, even when ξ is solvable, it is often found that it is satisfied by an infinite number of values of ξ. However, there will always be a smallest one of these different values. We choose the notation β_- α for the smallest solution of the equation:

ξ + α = β,

if it is actually solvable at all. In general β_- α is different to β - α, which always exists only if α < β.

Consider also the following equation between three integers β, α, γ:

β = γα

(where γ is the multiplier). It is easy to convince oneself that the equation:

β = ξα

has no solution other than ξ = γ, and that one can denote this γ by ^β⁄_α . On the other hand, one finds that the equation:

β = αξ

(where ξ is the multiplicand), if it is actually solvable for ξ, that often there are several solutions and perhaps infinitely many solutions, but one of the values for ξ is always the smallest, and this is designated by ^β⁄_α .

The numbers α of the second number-class are of two kinds:

1. those α which have a preceding member in the sequence, which is then α_-1 and I call these numbers of the first kind, and
2. those α which do not have a preceding member in the sequence, for which therefore there is no such α_-1 and I call these numbers of the second kind.

For example, the numbers ω, 2ω, ω^v + ω, ω^ω are of the second kind, whereas ω + 1, ω² + ω + 2, ω^ω + 3 are of the first kind.

Correspondingly, the prime numbers of the second number-class, which I defined in general terms in § 3, split into prime numbers of the second kind and of the first kind.

Prime numbers of the second kind are, in the order of their appearance in the second number-class (II), as follows:

ω, ω^ω, ω^ω2, ω^ω3, …

so that among all the numbers of the form:

φ = v₀ ω ^μ + v₁ ω ^μ - 1 + … + v_μ - 1 ω + v_μ

there is only the one prime number ω of the second kind. But one can not conclude from this comparatively sparse distribution of the prime numbers of the second kind that the set of all of them has a cardinal-number that is smaller than that of the number-class (II) itself; it will be found that this set has the same cardinal-number as (II).

The prime numbers of the first kind are initially:

ω + 1, ω² + 1, …, ω^μ + 1

These are the only prime numbers of the first kind that occur among the numbers previously designated as φ. The set of all prime numbers of the first kind in (II) also has the cardinal-number of (II).

The primes of the second kind have a property which gives them a very distinctive character. If η is such a prime number (of the second kind), then ηα = η whenever α is any number smaller than η. From this it follows that if α and β are any two numbers, both of which are smaller than η, then the product αβ is always smaller than η.

If we restrict ourselves here to the numbers of the second number-class, which have the form φ, the following addition and multiplication rules can be found for these. Let

φ = v₀ ω ^μ + v₁ ω ^μ - 1 + … + v_μ

ψ = ρ₀ ω ^λ + ρ₁ ω ^λ - 1 + … + ρ_λ

where we assume that v₀ and ρ₀ are different from zero.

Addition

1. If μ < λ, then one has:
   φ + ψ = ψ
2. If μ > λ one has:
   φ + ψ = v₀ω^μ + … + v_{μ - λ - 1} ω^{λ  + 1} + (v_μ - λ + ρ₀) + ρ₁ω^{λ  - 1} + ρ₂ω^λ - 2 + … + ρ_λ  
3. For μ = λ
   φ + ψ = (v₀ + ρ₀) ω^λ + ρ₁ω^{λ   - 1} + … + ρ_λ

Multiplication

1. If v_μ  is different from zero, then one has: φψ = v₀ω^μ + λ + v₁ω^{μ  +  λ  -  1} + … + v_μ-1ω^{λ   +  1} + v_μ ρ₀ω^λ + ρ₁ω^{λ   -  1} + … + ρ_λ If λ = 0, the last term on the right is v_μ ρ₀.  
2. If v_μ = 0, then one has: φψ = v₀ω^{μ  +  λ} + v₁ω^{μ  +   λ  -   1} + … + v_μ-1ω^λ + 1 = φω^λ

The decomposition of a number φ into its prime factors is as follows. Given:

φ = c₀ω^μ + c₁ω^μ₁ + c₂ω^μ₂ + … + c_δω^μ_δ

where

μ > μ₁ > μ₂ > · · · > μ_δ

and

c₀, c₁, … c_δ

are positive finite numbers other than zero, then:

φ = c₀ (ω^{μ - μ₁} + 1) c₁ (ω^{μ₁ - μ₂} + 1) c₂ … c_δ-1 (ω^{μ_δ - 1 - μ_δ} + 1) c_δ ω^μδ

If one thinks of c₀, c₁, … c_δ - 1 c_δ according to the rules of the first number-class, one then has the prime factorization of φ, since, as noted above, the factors ω^x + 1 and ω are themselves prime numbers. This decomposition of numbers of the form φ is uniquely determined, also with regard to the order of the factors, if one abstracts from the commutability of the prime factors within the individual c and if it is determined that the last factor has the cardinal-number ω or equal to 1 and that ω may only be a factor in the last position. I will write about the generalization of this decomposition into prime factors for arbitrary numbers α of the second number-class (II) at another occasion.

Go to Part 1     Go to Part 2     Go to Part 3