A Contribution to the Theory of Sets
“Ein Beitrag zur Mannigfaltigkeitslehre”
• English Translation •

A Contribution to the Theory of Sets

 

If two well-defined sets M and N can be set to correspond to each other uniquely and completely, element for element (which, if it is possible in one way, can always be done in many other ways), then in what follows we may say that these sets are of equal magnitude, or that they are equivalent. By a subset of a set M we mean any other set M′ whose elements are also elements of M. If the two sets M and N are not of equal magnitude, then either M will have the same magnitude as some subset of N or N will have the same magnitude of some subset of M; in the first case we say that M has a smaller magnitude than N, in the second case we say that M has a larger magnitude than N.

 

If the sets under consideration are finite, that is, they are composed of a finite number of elements, it is easy to see that the concept of magnitude corresponds to that of number and moreover to the concept of whole positive number, since two such finite sets are of equal magnitude if and only if the number of their elements is the same. A proper subset of a finite set is always of smaller magnitude than the set itself; but this relationship disappears completely for infinite sets, that is, sets composed of an infinite number of elements. From the mere fact that an infinite set  M is a subset of another N, or that it can be set in a unequivocal and complete correspondence to one, it should by no means be concluded that its magnitude is smaller than that of N. This conclusion is only justified if one knows that the magnitude of M is not equal to that of N; and the fact that N is a subset of M or can be set in an unequivocal and complete correspondence to such should not be regarded as sufficient to conclude that the magnitude of M is greater than that of N. To give a simple example, if M is the sequence of positive integers ν, and N is the sequence of positive even integers 2ν, then here N is a subset of M, but nevertheless M and N are of equal magnitude.

 

The sequence of positive integers ν offers, as can easily be shown, the smallest of all magnitudes that occur in infinite sets. Nevertheless the class of all sets which are of this smallest magnitude is an exceedingly rich and extensive one. This class includes, for example, all those sets which Herr R. Dedekind calls “finite fields” in his valuable and beautiful investigations into algebraic numbers. (Footnote: See also “Dirichlet’s Lectures on Number Theory”, second edition, Braunschweig 1871, p.425f.(Vorlesungen über Zahlentheorie, zweite Auflage).) Furthermore, the sets that I first analyzed are included here, which I have called “Point sets of the ν^th kind”. (Footnote: See Mathematical Annals, Vol.5, p.129 (Mathematische Annalen von Clebsch und Neumann).) Every set that appears as a simple infinite sequence, with the general term α_ν, obviously belongs here; but also the double sequence and in general the n‑fold sequence with the general term α_ν1, α_ν2, … α_νn (where each ν₁, ν₂, … ν_n has the domain of all positive integers independently of each other) belong to this class. On an earlier occasion it was also proved that the set (ω) of all real (and one could also add, all complex) algebraic numbers can be considered in the form of a sequence with the general term ω_ν, which means only that the set (ω) as well as each infinite subset of it have the magnitude of the entire sequence of numbers.

 

With regard to sets of this class, the following easy-to-prove theorems hold:

“If M is a set of the magnitude of the sequence of positive integers, then every infinite subset of M has the same magnitude as M.”

“If M′, M′′, M′′′… is a finite or simple infinite sequence of sets, each of which has the magnitude of the sequence of positive integers, then the set M which results from the union of the subsets M′, M′′, M′′′… has also the same magnitude.”

In the following, the so-called continuous, n‑fold spaces will be analyzed with regard to their magnitudes.

 

The assumptions which Riemann (Footnote: See Riemann’s collected mathematical works. Leipzig 1876. p.254f (Riemanns gesammelte mathematische Werke).) and Helmholtz (Footnote: See Helmholtz, “About the factual foundations of geometry”. Heidelberg yearbook 1868, no.46 and 47 (Über die tatsächlichen Grundlagen der Geometrie. Heidelberger Jahrbücher), and
“On the facts underlying geometry” by the same author, Goettinger News 1868, no.9 (Über die Tatsachen, welche der Geometrie zugrunde liegen. Nachr. Ges. Wiss. Göttingen, Math.-physik. Kl. 1868, Nr.9), and
“Popular lectures” by the same author, Vol 3, Braunschweig 1870, p.21f (desselben Verfassers populäre Vorträge, H.3, S.2lf. Braunschweig 1876).) and others since (Footnote: See J. Rosanes, “About the latest investigations into our view of space”, Breslau, 1871, p.13 (Über die neuesten Untersuchungen in betreff unserer Anschauung vom Raume), and
O. Liebmann, “On the analysis of reality”. Strassburg, 1876, p.58 (Zur Analysis der Wirklichkeit), and
B. Erdmann, “The axioms of geometry”, Leipzig, 1877, p.45 (Die Axiome der Geometrie).) made about the hypotheses on which geometry is based began, as is well known, from the concept of an n‑fold extended, continuous space where its essential characteristic is the fact that its elements depend on n independent, real, continuous variables x₁, x₂, … x_n , so that for each element of the space there is a possible system of values x₁, x₂, … x_n, but also conversely, every admissible system of values x₁, x₂, … x_n includes its own extent of variability. As can be seen from the course of those investigations, the assumption was also made, generally implicitly, that the underlying correspondence of the elements of the space to the system of values x₁, x₂, … x_n is a continuous one, so that for each infinitely small change of the system of values of x₁, x₂, … x_n there is an infinitely small change of the corresponding element and conversely every infinitely small change of an element corresponds to a change in the value of its coordinates. For now, it may be left as an open question as to whether this assumption is to be regarded as sufficient, or whether it should be supplemented by even more specialized conditions, so that the intention behind the concept of an n‑fold, continuous space, such that it can be considered to be secure against any contradiction, is intrinsically consistent. (Footnote: The answer to this question, to which we shall return on another occasion, does not seem to me to encounter any difficulties worth mentioning.)

 

Here it will be shown that if that requirement is dropped (i.e: if no restriction is made regarding the correspondence between a space and its coordinates), then that requirement which was considered by its authors to be essential (according to which an n‑fold continuous space is such that its elements are determined by n real, continuous coordinates that are independent of one another) becomes completely obsolete.

 

As our analysis will show, it is even possible to uniquely and completely determine the elements of an n‑fold extended continuous space by a single, real continuous coordinate t. It then follows that, if no assumptions are made regarding the nature of the correspondence, the number of independent, continuous, real coordinates that can be used for a unique and complete determination of the elements of an n‑fold extended continuous space can be defined to be any arbitrary number, and therefore that number is not to be regarded as an invariable characteristic of a given space. By asking myself the question whether a continuous space of n dimensions can be mapped uniquely and completely to a continuous set of one and only one dimension, such that each element corresponds to one and only one element of the other, it was found that this question must be answered in the affirmative.

 

Accordingly, a continuous surface can be clearly and completely related to a continuous line, and the same applies to continuous bodies and continuous structures with any number of dimensions.

 

Using the terminology introduced above, we can therefore say that the magnitude of any continuous n‑fold space is equal to the magnitude of a singly-extended continuous set, such as a finite continuous straight segment.

 

§ 1

Since two continuous structures that have the same number of dimensions can be clearly and completely related to each other by means of analytic functions, the purpose we are here pursuing (namely to demonstrate the possibility of unambiguous and complete associations of continuous structures with different numbers of dimensions), as one can easily see, is completely dependent on the proof of the following theorem:

 

As a consequence of this theorem there is another that comes to mind:

 

§ 2

To prove Theorem (A) we start from the well-known theorem that every irrational number e, 0 < e < 1, can be set in a completely determined manner in the form of an infinite continued fraction:

where α_ν are positive integers.

 

For every irrational number e, 0 < e < 1, there is a specific corresponding infinite sequence of positive integers α_ν and conversely every such sequence determines a specific irrational number e, 0 < e < 1.

 

If e₁, e₂, … e_n are n are variables independent of each other, where each of which can take any irrational numerical value in the interval (0…1), and each of these only once, then we set:

e₁ = (α_{1, 1}, α_{1, 2} , … α_{1, ν} , …),

. . . . . . . . . . . . . . . . . . . . . . .

e_μ = (α_{μ, 1}, α_{μ, 2} , … α_{μ, ν} , …),

. . . . . . . . . . . . . . . . . . . . . . .

e_n = (α_{n, 1}, α_{n, 2} , … α_{n, ν} , …).

 

These n irrational numbers uniquely determine an n + 1^th irrational number d, 0 < d < 1:

d = ( β₁ , β₁ , … β₁ , …),

by creating the following relationship between the numbers α and β:

 

But also vice versa: if one starts with an irrational number d, 0 < d < 1, then this determines the sequence of β_ν, and by virtue of (1) also the sequence of α_u,v (i.e: d uniquely determines the system of n irrational numbers e₁, e₂, … e_n). The following theorem results from this consideration:

 

§ 3

Following the proof of Theorem (C) in the previous section, it is now incumbent upon us to prove the following theorem:

 

Once this Theorem (D) has been proved, then following upon that and Section 2, we have that e₁, e₂, … e_n and d denote n + 1 variables that correspond uniquely and completely to the other variables x₁, x₂, … x_n and  t, where each one of these variables can take every real value ≥ 0 and ≤ 1 without restriction. Since in Section 2 an unambiguous and complete correspondence is established between the variable d and the set of n variables e₁, e₂, … e_n, in this way one obtains an unambiguous and complete correspondence of the single continuous variable t and the set of n continuous variables x₁, x₂, … x_n, by which the validity of Theorem (A) will be proven.

 

Hence, in the following we only have to deal with the proof of Theorem (D); for the sake of brevity, we will use a simple terminology, which we will first describe.

 

By a linear set of real numbers we want to understand any well-defined set of real, differing, (i.e: not equal) numbers such that any given number does not occur more than once as an element in a linear set.

 

The real valued variables encountered in the course of this inquiry are all such that the domain of each of them (i.e: the set of values which it can take) is a given linear set. We therefore do not want to particularly emphasize the assumption, which is made implicitly throughout the following. For two given variables a and b we shall say that they have no connection if no value that a can take is equal to some value of b (i.e: the two sets of values which the variables a, b can take have no elements in common), and it can be said that a and b are unconnected. (Footnote: Two sets M and N either have no connection if they have no common element; or they are connected by a certain third set P, namely by the set of the elements they have in common.)

 

If one has a finite or infinite sequence a′, a′′, a′′′, … , a^(v), … of well-defined variables or constants that have no pairwise connection, then a variable a can be defined by the fact that its domain arises from the combination of the domains of a′, a′′, a′′′, … , a^(v), …. Conversely, a given variable a can be decomposed in several ways into other a′, a′′, … which have no pairwise connection; in both of these cases we express the relation of the variable a to the variables a′, a′′, a′′′, … , a^(v), … by the following formula:

a ≡ {a′, a′′, a′′′, … , a^(v), …}

 

Hence the existence of this formula includes the following:

1. every value which any one of the variables a^(v) can assume is also a corresponding value of the variable a, and
2. every value which a can assume is also assumed by one and only one of the variables a^(v).

 

To explain this formula, for example, if φ is a variable containing all rational numerical values which are ≥ 0 and ≤ 1, e a variable containing all irrational numerical values of the interval (0…1), and finally x a variable which can assume all real (rational and irrational) numerical values that are ≥ 0 and ≤ 1, then we have that:

x ≡ {φ, e}

 

If a and b are two variables of such a kind that it is possible for them to correspond uniquely and completely to one another, in other words, if their domains are of equal magnitude, then we shall call a and b equivalent to one another and we indicate this by one of the two formulas:

a ~ b   or   b ~ a

According to this definition of the equivalence of two variables, it easily follows that a ~ a; furthermore that if a ~ b and b ~ c, then it is also always the case that a ~ c.

 

In the following analysis, the following theorem, the proof of which we may omit because of its simplicity, will be applied at various points:

 

 

§ 4

Our analysis has now progressed to the point that we are only left with the proof of Theorem (D) in Section 3. To achieve this goal, we suppose that all rational numbers which are ≥ 0 and ≤ 1 are in the form of a simple infinite sequence:

φ₁, φ₂, φ₃, …, φ_ν, …

where the general term is φ_ν. That this can be the case is shown quite simply as follows:

If ^p⁄_q is the irreducible form for a rational number that is ≥ 0 and ≤ 1 (i.e: where p and q are non-negative integers with the greatest common divisor 1), then let p + q = N. Then a definite, integral, positive value of N belongs to every number; conversely, only a finite number of numbers ^p⁄_q belongs to such a value of N. If the numbers ^p⁄_q are considered to be ordered that those belonging to smaller values ​​of N precede those belonging to greater values ​​of N, and furthermore, for any single value of N, the numbers ^p⁄_q follow one another according to their magnitude, the larger following the smaller, then every one of the numbers ^p⁄_q is in a very specific position in a simple infinite sequence, the general term of which is denoted by φ_ν. This theorem can also be concluded from an article I recently published (Footnote: See G. Cantor, “On a property of the set of all real algebraic numbers”, this journal, Vol.77, p.258f (Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen. Crelles Journal)
Translator’s note: see an online English translation of the article at On a Property of the Set of all Real Algebraic Numbers.) according to which the essential attribute (ω) of all real algebraic numbers is in the form of an infinite sequence:

ω₁, ω₂, …, ω_ν, …

with the general term ω_ν . This property of the attribute (ω) is carried over to the attribute of all rational numbers that are ≥ 0 and ≤ 1, because this set is a subset of that set. Now let e be the variable occurring in Theorem (D), which has to assume all real numerical values of the interval (0…1), with the exception of the numbers φ_ν.

 

Suppose further that in the interval (0…1) there is an infinite sequence of irrational numbers ε_ν which is bound only by the conditions that in general ε_ν < ε_ν + 1 and that lim ε_ν = 1 for ν = ∞; for example, let

ε_ν = 1 - ^√2⁄_2^ν

We denote by f a variable that can take any real value in the interval (0…1), with the exception of the values ε_ν and by g another variable that can take any real value in the interval (0…1), with the exception of the values ε_ν and φ_ν. We claim that:

e ~ f

In fact, according to the terminology of Section 3:

e ≡ { g, ε_ν }

f ≡ { g, φ_ν }

and since g ~ g, ε_ν ~ φ_ν, then by Theorem (E) we conclude that:

e ~ f.

 

Theorem (D), which is to be proved, is therefore reduced to the following proposition:

 

 

§ 5

We base the proof of Theorem (F) on the following Theorems (G), (H) and (J):

 

The simplest way of proving this Theorem (G) is to consider the curve in the diagram below, whose abscissas from 0 represent the magnitude x, and whose ordinates represent the magnitude y, and where the curve consists of the infinitely many parallel segments

a b, a′ b′, … , a^(ν) b^(ν), …

which become infinitely smaller as ν increases to infinity, and of the isolated point c, which those lines approach asymptotically. Here, however, the end points a, a′, … , a^(ν), … belong to the curve, whereas the end points b, b′, … . ,b^(ν), … are to be considered as excluded from it.

 

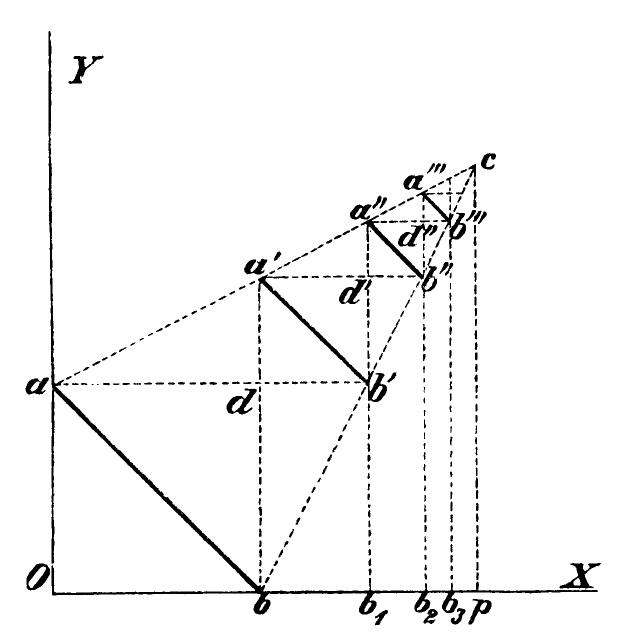
The lengths represented in the figure are:

Op = pc = 1

Ob = bp = Oa = ¹⁄₂

a^(ν)d ^(ν) = d ^(ν)b^(ν) = b_v-1b_v = ¹⁄_2^v+1

One can determine that while the abscissa x takes all values from 0 to 1, the ordinate y takes all these values with the exception of the single value 0.

 

Following on from this proof of Theorem (G), by the application of the transformation formulas:

one obtains the following generalization of Theorem (G):

 

From here we then arrive at the following theorem:

 

Indeed, if we let γ be some value between α and β, and we introduce four new variables ω′, ω′′, u′′ and z, where:

 

then we have:

ω ≡ ω′, ω′′

z ≡ ω′, u′′

 

However, as a consequence of Theorem (H) we have that:

ω′′ ~ u′′

and so we can conclude that :

ω ~ z.

Also by Theorem (H) we have that:

z ~ u

and consequently it follows that:

ω ~ u

which proves Theorem (J).

 

 

We can now prove Theorem (F) as follows: By the definition of the variables f and x in the statement of (F), we introduce certain auxiliary variables:

f ′, f ′′, f ′′′, … , f ^(v), …

and

x′, x′′′′, … , x^(2v), …

where:

 

If one adds the constant number 1 to the variables f ′, f ′′, f ′′′, … , f ^(v), …, then all these variables taken together have the same domain as f, that is, one has:

f ≡ { f ′, f ′′, f ′′′, … , f ^(v), … , 1}

We can also determine that:

x ≡ { f ′, x ′′, f ′′′, x ′′′′, … , f ^(2v - 1), x ^(2v), … , 1}

 

According to Theorem (J) however:

f ^(2v) ~ x ^(2v)

and furthermore:

f ^(2v - 1) ~ f ^(2v - 1) and 1 ~ 1

therefore, because of Theorem (E) in Section 3 we have that:

f ~ x

which was the conjecture to be proved.

 

 

§ 6

I now want to give a shorter proof of Theorem (D). The reason for not using only this proof is because the auxiliary lemmas (F), (G), (H), (J), which were used in the more complex proof, are of interest in themselves.

 

Let x, as before, be a variable which can take any real value in the interval (0…1), including the endpoint values; Let e be a variable which has the domain only of irrational values in the interval (0… 1). The conjecture to be proved is that x ~ e.

 

We consider the rational numbers ≥ 0 and ≤ 1 as in Section 4, in sequence form with the general term φ_ν where ν traverses through the sequence of numbers 1, 2, 3, … . Furthermore, we assume some arbitrary infinite sequence of only irrational and mutually different numbers in the interval (0…1) and we let the general term of this sequence be η_ν  (e.g: η_ν = ^√2⁄_2^ν).

 

Let h be a variable which can take on any value in the interval (0…1) with the exception of φ_ν and η_ν . As in Section 3 the terminology used is:

and

e ≡ { h, η_ν }

We can also write this last formula as follows:

We can note that:

h ~ h ;    η_2ν ~ η_2ν - 1 ;    φ_ν ~ η_2ν

and applying Theorem (E) from Section 3 to the two formulas (1) and (2) we have that:

x ~ e

which was the conjecture to be proved.

 

 

§ 7

For the proof of Theorem (A), the idea suggests itself of choosing the infinite decimal representation format instead of the sequence formula that is used. Although it might appear that this method would lead more quickly to the required goal, it nevertheless involves a difficulty which I wish to draw attention to here, and which was the reason why I refrained from using decimal representation in this analysis.

 

For example, if you have two variables x₁ and x₂ and set:

x₁ = ^α₁ ⁄₁₀ + ^α₂ ⁄₁₀₀ + … + ^α_ν ⁄_10^ν + …

x₂ = ^β₁ ⁄₁₀ + ^β₂ ⁄₁₀₀ + … + ^β_ν ⁄_10^ν + …

with the proviso that the numbers α_ν and β_ν are integers ≥ 0 and ≤ 9, and from a certain ν onwards are not always a value of 0 (except when x₁ or x₂ are themselves equal to zero), then these representations of x₁ and x₂ must be uniquely determined in all cases (i.e: x₁ and x₂ determine the infinite number sequence α_ν and β_ν and vice versa). If you derive from x₁ and x₂ a number:

t = ^γ₁ ⁄₁₀ + ^γ₂ ⁄₁₀₀ + … + ^γ_ν ⁄_10^ν + …

by letting:

γ_2ν - 1 = α_ν  and γ_2ν = β_ν  for ν = 1, 2, …

this does define a unique relationship between the system of x₁ and x₂ and the single variable t since a single set of values for x₁ and x₂ gives a specific value of t. However the fact to be considered here is that the variable t does not take on all the values of the interval (0…1); it is restricted in its variability, while x₁ and x₂ are not subjected to any restriction within that same interval. All values of the series sum:

^γ₁ ⁄₁₀ + ^γ₂ ⁄₁₀₀ + … + ^γ_ν ⁄_10^ν + …

where from some ν > 1 onwards all of γ_2ν - 1 or all of γ_2ν have the value zero must be considered to be excluded from the domain of t because such would lead to excluded decimal representations, namely finite representations of x₁ or x₂ .

 

 

§ 8

Having completed the intended analysis in the preceding paragraphs, there is now an opportunity to expand somewhat on the above. Theorem (A) and also Theorem (B) can be generalized, where continuous spaces of an infinitely large number of dimensions have the same magnitude as continuous sets of one dimension. However, this generalization is essentially reliant on one assumption, namely that such infinitely many dimensions themselves form a set which has the magnitude of the complete positive number sequence.

 

Instead of Theorem (A) we have the following:

 

By the help of Theorem (D) in Section 3 this proposition (A′) is reduced to the following:

 

The easiest way to prove Theorem (C′) is to use the continued fraction expansion as in Section 2, where:

e_ν = (α_{ν, 1}, α_{ν, 2} , … α_{μ, ν} , …) for ν = 1, 2, …

and

d = (β₁, β₂ , … β_λ, …)

establish a relationship between the integer positive numbers α and β, namely:

α_{μ, ν} = β_λ

where

λ = u +  

( μ + ν - 1)( μ + ν - 2)  

2

It is easily shown that the above function has the remarkable property that it represents all positive integers once and one only once if μ and ν can take the values of every positive integer value independently of one another.

 

With Theorem (A′), however, it now seems that a limit has been reached as to the possibility of any further generalization of Theorem (A) and the consequent conclusions.

 

Since it has been demonstrated that for an extraordinarily rich and wide range of spaces that they have the property that they can be uniquely and completely made to correspond to a bounded, continuous straight line or any part of it (by a part of a line we mean any subset of its points), then the question arises as to how the various parts of a continuous straight line (i.e: the various infinite subsets of points within it) are related as regards their magnitude. We can detach this problem from its geometric associations and consider, as already discussed in Section 3, that a linear set of real numbers defines every conceivable example of an infinite number of real numbers that are different from one another, so the question arises as to how many and into which classes the linear sets can be broken down, if sets of equal magnitude belong to a single class, and sets of different magnitudes are in different classes. By means of an inductive procedure, the presentation of which we shall not go into in detail here, this leads to the proposition that the number of classes of linear sets resulting from this principle of division is finite, namely that it is equal to two.

 

According to the above, the linear sets would consist of two classes: (Footnote: That these two cases are in fact different follows from what is proved in § 2 of the previously cited work (This Journal Vol.77 p.258f ), according to which, if there is a valid infinite sequence ω₁, ω₂, …, ω_v, …, then in any given interval (α … β) there can always be numbers μ found that do not occur in the given sequence.
Translator’s note: see an online English translation of the article at On a Property of the Set of all Real Algebraic Numbers.)

the first of which includes all sets which can be given by a function with a free variable ν, where ν has the domain of all positive integers,

while

the second class embraces all those sets which can be given by a function with a free variable ν, where ν has the domain of all real values ≥0 and ≤1.

 

Corresponding to these two classes, therefore, only two magnitudes occur for the case of the infinite linear sets; we defer the detailed examination of this question to a later occasion.

 

---

 

Footnotes:

 

---