The Balls in the Urn Paradox (Ross–Littlewood)

Page last updated 22 Nov 2025

This paradox was originally described by mathematician John Littlewood in his 1953 book Littlewood’s Miscellany, John Edensor Littlewood, A mathematician’s miscellany, London Methuen, 1953. and was also included by Sheldon Ross in his 1988 book A First Course in Probability. Sheldon Ross, A First Course in Probability 9th Edition. Pearson, 2014

The question as posed in Ross’s book is:

Suppose that there is an infinitely large urn and an infinite collection of balls each labeled with a unique number, 1, 2, 3, … . Consider the following process:

At 60 seconds before noon, balls numbered 1 through 10 are placed in the urn and ball number 10 is withdrawn. (we assume that the withdrawal takes no time.) At 30 seconds before noon, balls numbered 11 through 20 are placed in the urn and ball number 20 is withdrawn. At 15 seconds before noon, balls numbered 21 through 30 are placed in the urn and ball number 30 is withdrawn. And so on, and so on…

The question is: How many balls are in the urn at noon?

Ross says that the answer is clear, and is what most people would say - there is an infinite number of balls in the urn. This is in accordance with most people’s intuition, based on the fact that at each step more balls are added than are being removed.

Muddying the waters: Round 1

However, the question is now extended to the situation where at step 1, balls 1 through 10 are inserted into the vase, and ball number 1 is then removed. And at step 2, balls 11 through 20 are inserted, and ball 2 is then removed. And so on.

According to Ross & Littlewood, every ball labeled n that is put into the vase is eventually removed in a subsequent step, the step n, and hence, by noon the vase must be empty.

It’s easy to see the fallacy. Whether the balls are numbered or not is irrelevant. One could just as easily set the balls out in a line when putting the balls into the urn (the urn is infinitely large anyway) and simply remove according to the position on the line. Then the balls are completely identical, and it now means that the claim is now that it makes a difference to the result depending on where in the line you remove the ball from! The process is an infinite unending process that is not completed (the reference to hypothetical “time” in the description is a red herring, see Time as a red herring below). Because it is an infinite unending process, to make a calculation requires applying a limiting condition. Since the value in the problem which does not reach a finite endpoint value is n, then the limiting condition must be a condition which applies as n → ∞.

So what value are we going to calculate as n → ∞? Well, we can calculate the number of balls remaining in the urn as n → ∞. It’s obvious that after each step n (regardless of which ball is actually removed at that step) there are 9n balls remaining in the vase. And the limit of 9n as n → ∞ is infinite, or it might be better to say that there is no upper limit to the value of 9n. Hence there is no upper limit to the number of balls in the urn as the process continues indefinitely.

And we can also calculate the number of balls removed as n → ∞. It’s absurdly simple - as n → ∞ the number of balls removed approaches infinity. So the number of balls remaining in the urn and the number of balls removed, in the limit, become infinite.

Of course, the problem is that we cannot assign any number to any ball when calculating the limit. But this simply demonstrates that there is not necessarily a valid limit state for every definition that involves some reference to infinite quantities. In the case of the balls, it is clear that at each iteration, the total quantity of balls in the urn increases. Hence the notion that, even though at every iteration the numbers of balls in the urn increases without limit, the limit state is an urn with no balls is simply absurd. There simply is no valid limit state in which the balls are numbered. In an actual physical situation, each ball would have to become bigger and bigger as the iterations proceed, in order that a number can be physically imprinted in some way on the ball. So if there could be a limit state, each ball would have to be infinitely large, and the urn would have to be infinitely large and at the same time larger than the collection of infinitely many infinitely large balls. This is a contradiction, since it requires a limitlessly large entity to be larger than the combined size of infinitely many limitlessly large entities. Of course, there can be no actual physical situation where there are infinitely many infinitely large balls.

The Duplicate Urn

Another way to see the fallacy in Ross’s argument is given by the following;

Extraneous physical references

We can remove the references to the physical world of balls and urns, giving us the scenario where we have an algorithm, where at each step n, the numbers between 10n − 9 to 10n inclusive are added to a set, and the number n is removed from the set. Clearly, the recursive process never terminates, and the number of elements in the set continues to increase and never decreases. By simply removing the erroneous assumption that the process somehow magically terminates, we remove any apparent contradiction. It is a straightforward matter to define a function from this algorithm, and which defines the numbers in the set for any given n as the numbers from n + 1 to 10n. Of course, the n of this function is always finite, and there is no valid limit state for this function as n increases.

On the other hand, a definition of a set, also without any physical situation and without any recurring process, consisting of all subsets {n to n + 9} less all subsets {n} defines a total of zero elements. Of course, this is a completely different definition, and it does not entail any unending algorithmic process and which is an essential requirement of the initial definition of the scenario.

Muddying the waters: Time as a red herring

It is a fallacy to believe that the “time” referred to in the definition of the problem refers to time that we encounter in the real world, and that the hypothetical “time” in the problem reaches noon (and proceeds in the same way as real world time beyond noon). But the process, by definition, never completes - there are infinitely many steps.

So ask the question: Does the definition imply that noon is reached?

Answer: No, it doesn’t.

In fact, over 2000 years ago Zeno showed that what we encounter in the real world as “time” cannot be infinitely subdivided into forever decreasingly small segments - because if we assume that it could be, we end up with contradictions that are known as Zeno’s paradoxes. Part of the problem with the balls in the urn is that some people think of the word “time” where it occurs in the problem as though it is real time as we perceive it, but where there is no limit to how small it can be sub-divided.

While the problem is posed in terms of real physical balls and real physical urns, the fact is that the intervals of the hypothetical “time” in the problem become impossibly small for any real physical manipulating of the balls, regardless of how small the balls are. In the problem, “time” is simply a hypothetical mathematical dimension, where one can think of it in the same way as a physical length, and one can see that the “time” noon is never reached by the process - the definition only defines that this hypothetical “time” comes closer and closer to it without ever being reached. To understand this, we can consider the situation in terms of a dimension of distance instead of a dimension of “time” with its associated intuitive aspects.

So, suppose we have the situation where an elf, with urn in hand, advances the tip of his toes to a specific distance at each step that he moves. For the first step he moves half a unit, for the next step a quarter unit, for the next step an eighth of a unit, and so on. Every step that he takes has an associated number, as each step is numbered as 1, 2, 3, … , and every number is associated with some step. Now, none of the steps is the step where the tips of the elf’s toes actually reach one unit. So how could the notion arise that the elf actually reaches a distance of one unit? There is no step that actually reaches that point, and the notion that it does is absurd nonsense. On the other hand the notion that the limiting value of the distance moved by the elf is one unit - and which is never actually attained - is perfectly logical.

And, in exactly the same way as the hypothetical elf can never reach one unit, never mind move further than one unit, the hypothetical infinitely divisible “time” can never reach noon, much less move past noon.

Of course, we acknowledge that in our perception of the world we live in, time continues and does not stop. So when the original problem is posed in terms of the word “time”, there is a tendency to intuitively assume that in the problem, there is something that is referred to by the word “time”, and which progresses exactly as time does in real life. But intuition should never take precedence over logic.

Asking how many balls will be left at noon invites one to assume that there is no contradiction between the definition given and the assumption that noon can be reached by the definition.

The paradox is a result of an inherent contradiction in the question that is asked. The fact that most people answer that there will be infinitely many balls in the urn is simply because they assume that the poser of the question intended it to be meaningful, and this response is the best way of dealing with the contradiction that results from that assumption.

Muddying the waters: Round 2

In his book, Ross muddies the waters even further by considering if the choice of which ball removed at each step is completely random, and calculating the probability of a ball of number n having being removed by some step m. Obviously, as the number of steps increases, the probability of that particular ball being removed, on or before that step, becomes ever greater. The limit of this probability is a probability of 1. But that is a limit that is not actually reached by the unending infinite process.

On the other hand, for any ball, the probability that there is some step n at which it is removed is, of course, 1 - it is a certainty. And the converse, the probability that there is no step n at which it is removed is 0. It takes Ross several equations to come to this outstandingly obvious conclusion.

Ross takes that probability of 0 for one ball, and applies it to all the balls, and comes up with a result that the total probability that for every ball, there is no step at which it is not removed is also 0. Again an outstandingly obvious result.

But it is also the case that, for every step  n, there remain 9n balls in the urn, all with larger numbers than  n. The paradox only arises when Ross takes this simple statement and twists the meaning to read:

“The probability that the urn is not empty at 12 PM is 0.”

Question:

Where does Ross rake up this conclusion from? Where in his equations is there any mention of time, or 12 PM or noon?

Answer:

Nowhere in his equations is there any mention of time in any form whatsoever, see the Appendix below. All they refer to is the probability of a ball being removed at some step in a limitless recursive process that never terminates. Ross’s equations are simply a sham facade that have absolutely nothing to do with Ross’s promotion of a Platonist agenda that an infinite process can in some way “finish”. He might as well have said:

“The probability that the urn is not empty when the endless recursive process ends is 0.”

It is interesting that there is a substantial discussion of the paradox at StackExchange: Balls in an urn where there is intense debate about the equations - there is one respondent who hits the nail on the head, see What’s the best explanation we can give to them to solve these conflicting intuitions? It is also interesting that it has been given hardly any up-votes, the voters preferring instead to wallow in Platonist fantasy land. And although Zeno, over 2000 years ago, pointed out that time that we encounter in the real world cannot be infinitely divisible, and that if you assume it does, you end up with contradictions - Zeno’s paradoxes - these people simply ignore Zeno’s logic and believe that they can churn out unsolvable conundrums by adding notions of real world balls and urns to Zeno’s scenarios. These Platonists mock other people if they prefer the application of logic over the pseudo-mathematical arguments that these Platonists present, but the irony is that the Platonists’ own arguments involve illogical intuitive beliefs that the infinite process can somehow magically terminate. For more on the problems inherent in Platonism, see Platonism and The Myths of Platonism.

You could just as easily ask the probability that, for any ball of number n, there will be balls left in the urn that have a number either less or greater than n - for which the probability is 1; and for any ball of number n, there will be no balls left in the urn that have a number either less or greater than n is a probability of 0. Applying that to all balls gives the opposite result to the above result.

And more…

For another example of a contradiction arising from the notion that an infinitely recursive process can somehow “complete”, see The Platonist Rod paradox.

Other paradoxes

Appendix: Sheldon Ross’s equations

The following is from Example 6a, Probability and a paradox in Chapter 2 Axioms of Probability, in Sheldon Ross’s book A First Course in Probability 9th Edition. Pearson, 2014: PDF A First Course in Probability

 

Define E_n to be the event that ball number 1 is still in the urn after the first n withdrawals have been made. Clearly

 

 

[To understand this equation, just note that if ball number 1 is still to be in the urn after the first n withdrawals, the first ball withdrawn can be any one of 9, the second any one of 18 (there are 19 balls in the urn at the time of the second withdrawal, one of which must be ball number 1), and so on. The denominator is similarly obtained.]

 

Now, the event that ball number 1 is in the urn at 12 PM In fact these symbols make no reference whatsoever to 12 PM, nor to time in any form. What they actually refer to is the totality of events where n is not the step where the ball 1 is removed. That’s all. is just the event

 

 

Because the events E_n, n ≥ 1, are decreasing events, it follows from Proposition 6.1 that

 

P{ball number 1 is in the urn at 12 PM}

 

 

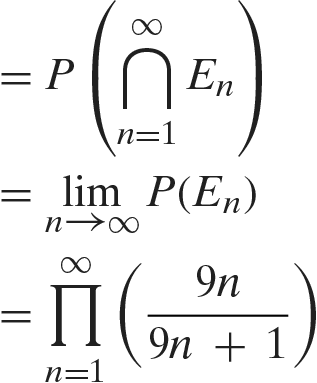
We now show that

 

 

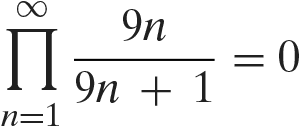
Since

 

 

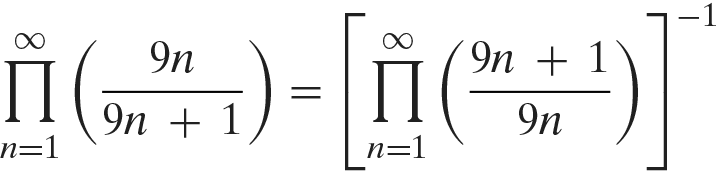
this is equivalent to showing that

 

 

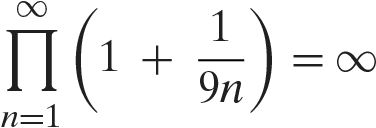
Now, for all m ≥ 1,

 

 

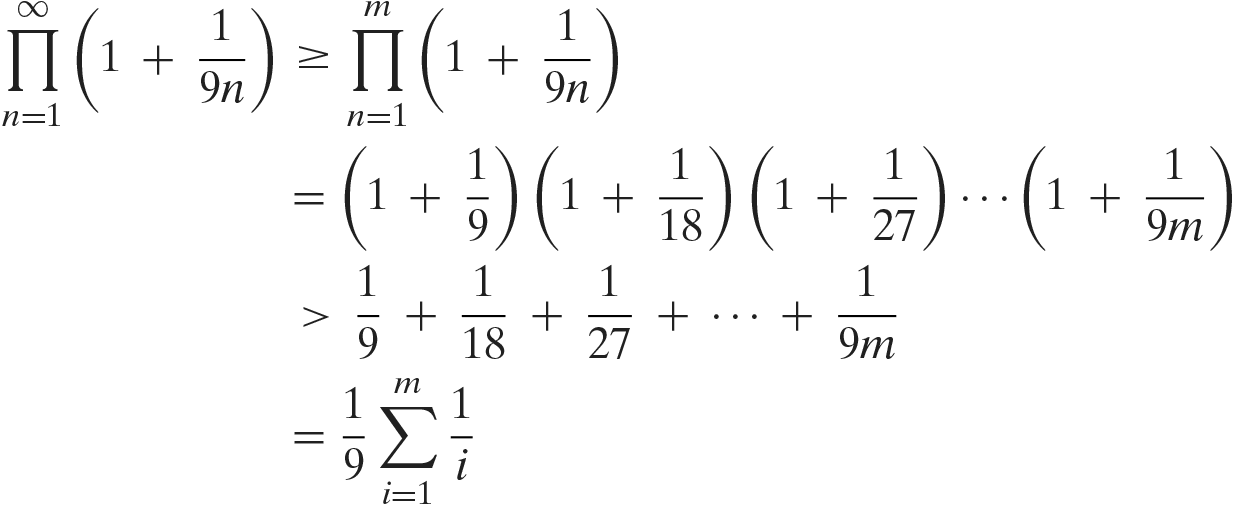
Hence, letting n → ∞ and using the fact that

 

 

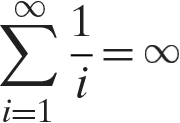
yields

 

 

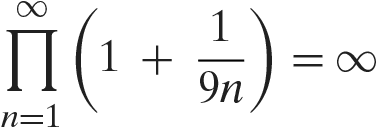
Thus, letting F_i denote the event that ball number i is in the urn at 12 PM, As previously noted, in fact F_i makes no reference whatsoever to 12 PM, nor to time in any form. What they actually refer to is the totality of events where there is not a step n where the ball i is removed. we have shown that P(F₁) = 0. Similarly, we can show that P(F_i ) = 0 for all i.

 

(For instance, the same reasoning shows that

for i = 11, 12, … , 20.)

 

Therefore, the probability that the urn is not empty at 12 PM Again, we must note that these equations make no reference whatsoever to 12 PM, nor to time in any form. What they actually refer to is the total probability of events where there is not a step n where the ball i is removed.

 

 

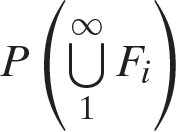
satisfies

 

 

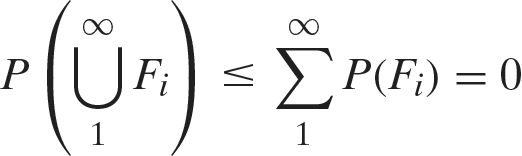
by Boole’s inequality. Thus, with probability 1, the urn will be empty at 12 PM. Yet again, it must be stressed that the above equations make no reference whatsoever to 12 PM, nor to time in any form.