Footnotes:
Glossary
Page last updated 13 May 2023
Lemma
A lemma is a theorem that is usually not considered a primary result in itself, but which is useful as a step towards proving another theorem.
Natural numbers
The term “natural numbers” is usually used to refer to the non-negative whole numbers, 0, 1, 2, 3, …, but it is also sometimes used to mean only the positive whole numbers 1, 2, 3, … .
Integers
The integers include the negative whole numbers: … -3, -2, -1, 0, 1, 2, 3, …
Number Systems
There are many different ways of denoting numbers. The system we use today for almost everything is the decimal system, which uses the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. However, there is no particular reason to use the decimal system other than it is the system that has become universally accepted today. Most historians believe that the decimal system arose because we have ten fingers, and long ago, fingers were used as a handy portable counting tool. As a matter of historical interest, 5000 years ago the Sumerians of ancient Mesopotamia also used a system in which they counted by 60s (the sexagesimal system). The Babylonians developed this into a fairly sophisticated system, from which we get our 60 seconds in a minute, and sixty minutes in an hour, and 360 degrees in a circle (360 = 6 x 60, and degrees are divided into 60 minutes, and each minute of arc is divided into 60 seconds).
Unary System
The most basic number system is the Unary number system. This system uses only the digit 1 and no other digits. To represent a number in the unary system, you simply write down as many 1s as the number you want. For example: 1111111 represents 7, 111 represents 3, and 111111111 represents 9. Note that in the unary system the position of any digit is immaterial. In other systems, the positions of the digits are of fundamental importance. Also note that in the unary system, there is no representation of the number zero. Unary systems were the first number system used by man. It was a simple way to make a record of a count and is still used today, called tallying.
The modified Unary system with the number zero is the same as the Unary system, except that there is a symbol for zero. There are two types of such systems, representing numbers as:
0, 1, 11, 111, 1111, 11111, …
or
0, 10, 110, 1110, 11110, 111110, …
Note that the latter method is commonly used in formal systems, except that a symbol such as s is usually used instead of 1, so that you might have 0, s0, ss0, sss0, ssss0, sssss0, …
Decimal system
In the standard decimal system we use the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 to write down numbers. In the binary system we only use the digits 0 and 1 to write down numbers. In the decimal system, you can think of a number as being organized into columns, so that 2973 gives:
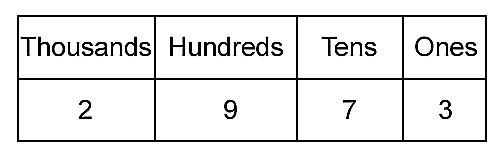
The leftmost column is for ones, the next column is for tens, the next for ten times ten, the next ten times ten times ten, and so on. So the positions tell us that 2973 means 2 thousands plus 9 hundreds plus 7 tens plus 3 ones. So the number 9372 is quite different to the number 2973, although the symbols used are the same.
In unary notation the number 2973 would be a sequence of 2973 1’s following each other, 11111111111111111111…
which is quite a handful, so you can see why we use a system such as the decimal system to deal with numbers in a manageable way. The decimal system is also called the base 10 number system.
Binary system
The binary system is also called the base 2 number system. It works under exactly the same principles as the decimal system, only the positions of the digits represent multiples of 2s rather than multiples of 10s. And instead of having 10 distinct digit symbols, it has only two digit symbols, 0 and 1.
As for the decimal system, you can think of a number as being organized into columns, so that the binary number 1011011 gives:
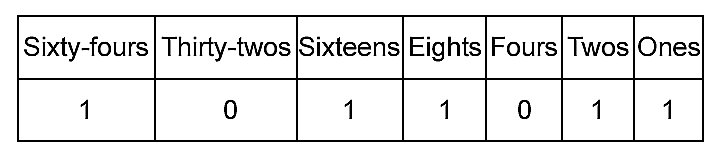
The leftmost column is for ones, the next column is for twos, the next for two times two, the next two times two times two, and so on. So the positions tell us that 1011011 means:
Sixty-four plus sixteen plus eight plus two plus one, which is 91 in decimal notation. Binary notation seems difficult only because we aren’t used to it.
Binary expansion
A representation in the binary system of a real number between 0 and 1 (see also Binary system). Whereas a decimal number uses all of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a binary expansion only uses the digits 0 and 1.
A binary expansion or a decimal expansion is simply a convenient way of writing fractions:
0.1 in decimal notation means 1⁄10 (a tenth)
0.01 in decimal notation means 1⁄100 (a hundredth)
0.001 in decimal notation means 1⁄1000 (a thousandth)
Similarly,
0.1 in binary notation means a half, which in the binary system is written as 1⁄10
0.01 in binary notation means a quarter, which in the binary system is written as 1⁄100
0.001 in binary notation means an eighth, which in the binary system is written as 1⁄1000
One-to-one Correspondence / Bijection
If one set of things can be matched up with another set of things, so that everything in the first set is paired up uniquely with one and only one thing in the second set, then that is often called a one-to-one correspondence, or a bijection, or for some cases, a list or a sequence. When this is the case, then there is no thing in the first set that is not matched to some thing in the second set, and there is no thing in the second set that is not matched to a thing in the first set - and every thing is matched up to one and only one thing from the other set.
We can also have a one-to-one correspondence between limitlessly large sets. For example, if we have the set of all natural numbers, {0, 1, 2, 3, …} and the set of all even numbers {2, 4, 6, …}, and we define the pairing to be such that an element of the second set is given by adding one to the value of each element of the first set, and then multiplying by two, that defines a one-to-one correspondence of the two sets as (0, 2), (1, 4), (2, 6), (3, 8), …
It should be noted that the impossibility of a one-to-one correspondence between two infinite sets depends on the properties of the elements of the sets, rather than anything to do with the quantities of elements of the sets, see One-to-one Correspondences and Properties.
The term ‘list’, or sequence, or enumeration, is often used to refer to a one-to-one correspondence to natural numbers, so that to say that a set can be ‘listed’ or ‘enumerated’ means that there can be a one-to-one correspondence between that set and the set of natural numbers. Obviously, for a one-to-one correspondence such as the one above, for the natural numbers and the even numbers, we can never actually write out such a list in its entirety; the list must be defined rather than written as an actual written down list.
Denumerable
For a given infinite set, if a one-to-one correspondence can be defined between the elements of that set and the set of all natural numbers, then the set is said to be denumerable, otherwise it is a non-denumerable set. This means that for every element in the set there is one, and only one matching natural number, and there is no natural number that does not have a corresponding element in the set. Such a one-to-one correspondence can be called an enumeration or simply a list or a listing.
Note that the term countable is often used instead of denumerable, and uncountable instead of non-denumerable - I prefer not to use the terms countable and uncountable, since in ordinary language uncountable is often used to mean finite (such as describing a large quantity of physical things), whereas the intended mathematical meaning is that the set is infinite but a one-to-one correspondence cannot be defined between the set and the natural numbers.
Other terms used to denote the same meaning as denumerable are listable and enumerable.
Surjection
A surjection from a set X onto a set Y is when every element of X is matched to an element of Y. Note that there can be more than one element in X that maps to an element of Y, so that it is not necessarily the case that every element of Y has a matching element in X. If every element of Y also has a matching element in X, then the surjection is also a bijection or a one-to-one correspondence, see above. The images are examples of surjections for finite sets.
It should be noted that the impossibility of a surjection between two infinite sets depends on the properties of the elements of the sets, rather than anything to do with the numbers of elements of the sets, see One-to-one Correspondences and Properties.
Primitive Recursive Relations
This section is not intended to be a comprehensive explanation of primitive recursion, since the information is readily available elsewhere. Instead we will try to give the fundamental essentials of what primitive recursion entails.
When the free variables of a relation are substituted by specific numbers, the result of the substitution is a proposition that may be correct or incorrect. For a primitive recursive relation, when its free variables are substituted by specific numbers, the result of the substitution is a proposition - and this proposition, or else its negation, can always be proved to follow from the axioms of number theory by a method that always has a finite number of steps.
Similarly, when the free variables of a function are substituted by specific numbers, the result of the substitution is an expression that has a numerical value. For a primitive recursive function, when its free variables are substituted by specific numbers, the resulting numerical value can always be evaluated (according to the axioms of number theory) by a method that always has a finite number of steps.
Note: There are functions and relations that can be calculated by a finite number of steps, but which are not primitive recursive - this is not explained by the simplified description above.
Use of Primitive Recursion in Incompleteness Proofs
Gödel used primitive recursive relations in his proof of incompleteness for two reasons:
- Because every (substituted) primitive recursive relation, or its negation, is provable from the axioms of number theory, and
- Because every primitive recursive relation can be expressed in the formal system.
When it is said that every primitive recursive relation can be expressed in the formal system, what this means is that:
For any primitive recursive relation with a free variables, there is a corresponding formula in the formal system which also has a free variable (and this also applies for relations with more than one free variable).
If the free variables of a primitive recursive relation are substituted by number values, then it can be proved by a finite number of steps if the relation is a correct or an incorrect proposition. Since there is a precise correspondence between the relation and a formula of the formal system, then if the relation is proven to be a correct proposition, the corresponding formula is also a correct proposition - and if the relation is proven to be an incorrect proposition, the corresponding formula is also an incorrect proposition.
Real numbers
Real numbers can be divided into rational numbers and irrational numbers. A fundamental property of any real number is that it can be set in order against any other real number. (Footnote: Real numbers are said to constitute an ordered field.) It either has to be bigger, or smaller, or than any other real number. The name ‘real’ was used because at that time, mathematics was considered to be a science that dealt principally with quantity, so that mathematics was the means by which quantities might be measured, and the real number system was the foundation for all such measurement.
Rational numbers
Rational numbers are numbers that can be represented as fractions. The name ‘rational’ comes from the fact that all such numbers represent a ratio. The numerator of a fraction is the upper term of the fraction, while the denominator is the lower term, and the value of the fraction is the value of the numerator divided by the denominator. Given any two rational numbers, there is always at least another rational number between those two numbers - in fact, there is no limit to how many rational numbers there can be between any two rational numbers.
However, despite this fact, there are real numbers other than the rational numbers - numbers for which there is no way they can be represented as a fraction - these are the irrational numbers.
Irrational numbers
An irrational number is the solution of a numerical equation where the solution cannot be represented as a rational number, but the value of the solution can be set in order against any other real number. An example of an irrational number is the square root of two - that is, the value which, when multiplied by itself, gives the value 2.
Exponent
When a number is multiplied by itself, the number of times that it is multiplied by itself is called the exponent. For example, if 5 is multiplied by itself 9 times, then 9 is the exponent, and this is denoted by a superscript, as 59. This is also called raising 5 to the power of 9.
Algebraic numbers
An algebraic number is a solution to what is called a polynomial equation. An example of a polynomial equation is 6x3 + 7x2y + 3y -2. The numbers multiplying the variables (x and y in the example) may only be integers. Algebraic numbers can be real numbers, or they can be complex numbers, see below.
Transcendental numbers
A transcendental number is an irrational number that is not algebraic. The common examples are π (Pi), which has a value of approximately 3.1416, and e (Euler’s number) which has a value of approximately 2.7183. A transcendental number cannot be expressed in terms of finitely many rational numbers, but can be expressed in terms of infinitely many rational numbers.
The real number line
The “real number line” is a hypothetical visualization of the set of real numbers, based on the fact that given any two real numbers, then one must be greater than the other if they are not identical. This hypothetical visualization assumes that one can visualize all real numbers simultaneously existing together thereby creating a hypothetical “line”; this notion has given rise to some rather unfortunate notions, see for example, “The Real Number Line”.
Complex numbers
A complex number is the sum of two parts, a real number part and an “imaginary” number part.
An imaginary number is a number that is a multiple of the imaginary unit, where the imaginary unit is the square root of minus 1. It is usually indicated by the small italic letter i. So, for example, 7i is an imaginary number. For more information see Wikipedia - imaginary numbers and Wikipedia - the imaginary unit.
So, for example, 57.9 + 8.3i is a complex number. For more information, see Wikipedia - Complex numbers.
The original reason the term “imaginary number” was used was because there does not appear to be any physical distance that corresponds to such a number. Despite that, imaginary numbers have numerous useful applications in science and engineering.
Transfinite Numbers
Transfinite numbers are numbers that are limitlessly large, but with the catch that some limitlessly large transfinite numbers can be larger than other limitlessly large transfinite numbers. If you think that’s absurd, then you probably aren’t alone, see Why do people believe weird things? Georg Cantor invented transfinite numbers in the late 19th century (see Cantor’s invention of transfinite numbers and Cantor’s religious beliefs and his transfinite numbers) and since that time, no useful application of these numbers has ever been found. For further discombobulation see Wikipedia - Transfinite numbers which tries to explain transfinite numbers as “numbers that are infinite in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite.” For further elucidation, see The Origins of Transfinite Numbers and Cardinal Numbers on this website.
Intervals
Degenerate interval: A degenerate interval of the real number line is an interval of that line that consists only of a single point; a non-degenerate interval is therefore an interval that consists of more than a single point, which means that every non-degenerate interval consists of infinitely many points, since there cannot be finitely many consecutive real numbers.
Open interval: An open interval is an interval that does not include the endpoints that define that interval. An example of an open interval is one whose endpoints are 1⁄3 and 1⁄2 is the set of all points between 1⁄3 and 1⁄2 but not including the points 1⁄3 and 1⁄2.
Closed interval: A closed interval is an interval whose endpoints are included in the interval.
Complete Interval: An interval of A is a complete interval if it is not a sub-interval of any interval of A apart from itself. For example, if a set X consists of two overlapping closed intervals, the interval with endpoints 1⁄5 and 1⁄3 , and the interval with endpoints 1⁄4 and 1⁄2 , then X consists of the complete closed interval with endpoints 1⁄5 and 1⁄2.
Well-ordering
The term “well-ordered set” is a term that refers to the assumption that all elements of any set can have a specific quantity of an indefinable variable property, where:
- no two different elements can ever have the same quantity of the property, and
- in every set there is always one element with the smallest quantity of that property.
The property is simply assumed to ‘exist’, even though, for example, in the definition of a mathematical system, there is no definition of that property - it is assumed to ‘exist’ completely independently of any human or machine. It is important to observe that the concept that is given this term “ordering” is not something which can be denumerable, nor is it a numerical ordering according to the numerical values of the elements. Similarly, the usage of the term “least element” with respect to this “ordering” does not mean that the element is the numerically smallest number of the set. For a full analysis see the page The Axiom of Choice and Well-Ordering.
The Complement of a set
Given some set U, then if a set A of some elements of the set U is defined, then its complement within U is the set of all elements that are in U but not in A. Such a complementary set is usually denoted by AC. Note: normally the set U is not explicitly referenced since its properties are evident by the context.
Syntax
Essentially, when we refer to the syntax of a language, we are referring to valid expressions of the language, as opposed to strings of symbols simply being objects that the expressions of the language refer to. In a valid syntactical expression some, but not all, of the symbols of the expression may be objects. (Footnote: In computer languages, objects of the language are usually called data.) Note that, for any object of the language, there can be a variable that has a domain that includes that object as a value. Variables of a logical language should never also be objects of that language.
As an example of the distinction of syntax and object, in English, the expression ‘The cat sat on the mat’ is valid syntax, where ‘cat’ and ‘mat’ are objects. The inherent ambiguity of natural languages such as English, means that there can be sentences where it is not clear whether a certain string of symbols is intended to be read as a valid syntactical expression or as an object. We might use quotation marks; for example, we might write, ‘The expression “The cat is black” has thirteen letters.’, and we use the quotation marks to indicate that the string of symbols within the quotation marks is intended to be an object to be referred to, rather than as part of the syntax of the overall sentence. We could equally well write, ‘The expression “kab ic aaT chest” has thirteen letters.’ which is also syntactically correct, but in this case it is obvious that the string of symbols within the quotation marks is not valid syntax of the language - and nor does it need to be for the overall sentence to be valid syntax. However, in English, there are no rules to prevent certain strings of symbols appearing at the same time to be valid syntactical expressions and also as objects. This ambiguity is the root source of many paradoxes of natural language.
For a language to be suitable for logical analysis, we would want to ensure that strings of symbols cannot at the same time be objects and valid syntactical expressions of that language.
Delimiters
For formal languages where no such ambiguity is allowed, there must always be a clear distinction between valid syntax and objects of the language, and so, in clearly defined formal languages, there will always be some method of distinguishing syntax and object. Generally this is achieved by the rules of the language which only allows certain combinations of symbols. Special symbols can be used in the same way as the quotation marks were used above and which indicate that the enclosed symbol combination is an object. Such symbols (or sequences of symbols) are called delimiters. By using such delimiters, the same string of symbols can be either part of the syntax of the language when not enclosed by delimiters, or when it is enclosed by delimiters, it is an object. In this way the delimiters maintain the distinction between the string as part of the normal syntax and as an object. Computer languages are examples of formal languages that use delimiters.
In terms of a meta-language and a sub-language, within the meta-language, every combination of symbols of the sub-language is an object - they are not part of the syntax of the meta-language. When delimiters are used, the symbol strings within the delimiters are effectively symbol strings of a sub-language, since as far as the meta-language is concerned, everything within the delimiters is an object.
Use-Mention
Many philosophers like to use the terms ‘use’ and ‘mention’, where to ‘use’ a word or phrase is to use it as part of the syntax of the language, whereas to ‘mention’ a word or phrase is to refer to it as an object. In other words, when we ‘mention’ a word, we are referencing it as an object (so effectively referring to it by a meta-language), whereas when we ‘use’ a word, that means the word is part of the normal syntax of a language.
The Halting Problem
The Halting problem is the question whether there is a general method that can be applied to any computer program and determine whether a computer that is run with that program will stop (halt) or keep running indefinitely on a given input.
It has been determined that there can be no such general method, first demonstrated by Alan Turing in his paper PDF On Computable Numbers…. See also The Halting Problem at the Brilliant web-site.
Consistent System
A consistent system is a system that can never result in a contradiction; no matter how many times the rules of the system are applied, a contradiction can never arise.




Rationale: Every logical argument must be defined in some language, and every language has limitations. Attempting to construct a logical argument while ignoring how the limitations of language might affect that argument is a bizarre approach. The correct acknowledgment of the interactions of logic and language explains almost all of the paradoxes, and resolves almost all of the contradictions, conundrums, and contentious issues in modern philosophy and mathematics.
Site Mission
Please see the menu for numerous articles of interest. Please leave a comment or send an email if you are interested in the material on this site.
Interested in supporting this site?
You can help by sharing the site with others. You can also donate at where there are full details.
where there are full details.